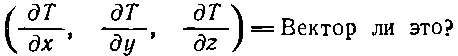 (2.11)
(2.11)
Ясно, конечно, что, вообще говоря, не из любых трех чисел можно составить вектор. О векторе можно говорить только тогда, когда при повороте системы координат компоненты преобразуются по правильному закону. Так что следует проследить, как меняются эти производные при повороте системы координат. Мы покажем, что (2.11) — действительно вектор. Производные действительно преобразуются при вращении системы координат так, как полагается.
В этом можно убедиться по-разному. Можно, например, задать себе вопрос, ответ на который не должен зависеть от системы координат, и попытаться выразить ответ в «инвариантной» форме. К примеру, если S= A· Bи если Аи В— векторы, то мы знаем (это доказано в вып. 1, гл. 11), что S — скаляр. Мы знаем , что S — скаляр, не проверяя, меняется ли он при изменении системы координат. Ему ничего иного не остается , раз он является скалярным произведением двух векторов. Подобным же образом, если мы знаем , что А— вектор, и у нас есть три числа B 1, B 2, В 3, и мы обнаруживаем, что
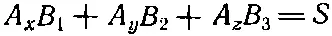 (2.12)
(2.12)
(где S в любой системе координат одно и то же), то три числа B 1, B 2, В 3обязаны быть компонентами В х, В у, В zнекоторого вектора В.
Рассмотрим теперь температурное поле. Возьмем две точки P 1и Р 2, разделенные маленьким расстоянием Δ R.Температура в Р 1есть T 1, а в Р 2она равна T 2, и их разница ΔТ=Т 2-Т 1.Температура в этих реальных физических точках, конечно, не зависит от того, какие оси мы выбрали для измерения координат. В частности, ΔT — тоже число, не зависящее от системы координат. Это скаляр.
Выбрав удобную систему координат, мы можем написать
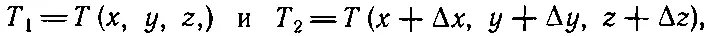
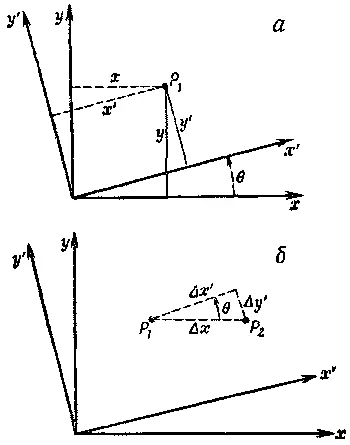
где Δx, Δy, Δz — компоненты вектора Δ R(фиг. 2.5).
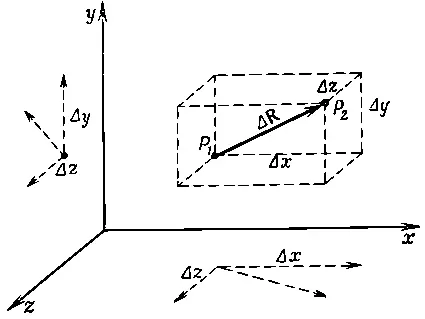
Фиг. 2.5. Вектор ΔR с компонентами Δх, Δу, Δz.
Вспомнив (2.7), напишем
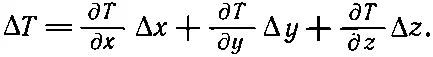 (2.13)
(2.13)
Слева в (2.13) стоит скаляр, а справа — сумма трех произведений каких-то чисел на Δx, Δy, Δz, которые являются компонентами вектора. Значит, три числа
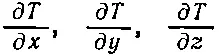
тоже х -, у - и z-компоненты вектора. Мы напишем этот новый вектор при помощи символа ∇ Т . Символ ∇(называемый набла) — это Δ вверх ногами; он напоминает нам о дифференцировании. Читают ∇T по-разному: «набла T», или «градиент T», или «gradT»:
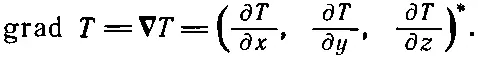
[4] В наших обозначениях выражение (а, b, с) представляет вектор с компонентами а, b, с. Если вам нравится пользоваться единичными векторами i, j и k, то можно написать
(2.14)
С этим обозначением (2.13) переписывается в более компактной форме
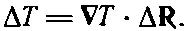 (2.15)
(2.15)
Или, выражая словами: разница температур в двух близких точках есть скалярное произведение градиента Т на вектор смещения второй точки относительно первой. Форма (2.15) также служит иллюстрацией к нашему утверждению, что ∇Т — действительно вектор.
Быть может, вы еще не убеждены? Тогда докажем иначе. (Хотя, вглядевшись внимательно, вы увидите, что это на самом деле то же самое доказательство, только подлиннее!) Мы покажем, что компоненты ∇Т преобразуются абсолютно так же, как и компоненты R, а значит, ∇Т — тоже вектор в соответствии с первоначальным определением вектора в вып. 1, гл. 11. Мы выберем новую систему координат х', у', z' и в ней вычислим ∂ T /∂ x ', ∂ T /∂ y ', ∂ T /∂ z '. Для простоты положим z=z', так что о третьей координате мы можем позабыть. (Можете сами заняться проверкой более общего случая.)
Выберем систему х', у', повернутую относительно х, y-системы на угол θ (фиг. 2.6, а).
Читать дальше

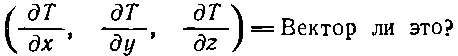 (2.11)
(2.11)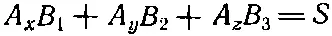 (2.12)
(2.12)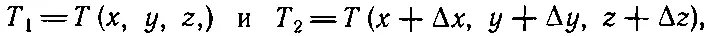

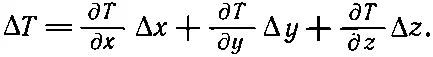 (2.13)
(2.13)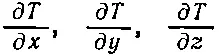
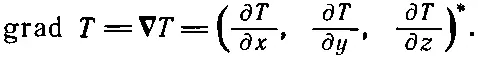
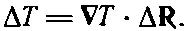 (2.15)
(2.15)




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)


