Фиг. 2.6. Переход к повернутой системе координат (а) и частный случай интервала ΔR ,параллельного к оси х (б).
Координаты точки (х, у) в штрихованной системе имеют вид
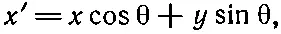 (2.16)
(2.16)
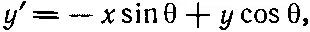 (2.17)
(2.17)
или, решая относительно x и y,
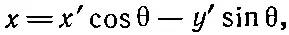 (2.18)
(2.18)
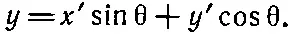 (2.19)
(2.19)
Если всякая пара чисел преобразуется так же, как x и y, то она является компонентами вектора.
Рассмотрим теперь разницу в температурах двух соседних точек Р 1и Р 2(фиг. 2.6, б). В координатах х, у запишем
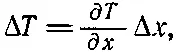 (2.20)
(2.20)
так как Δу=0.
А в штрихованной системе? Там мы бы написали
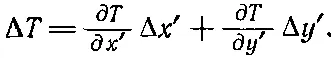 (2.21)
(2.21)
Глядя на фиг. 2.6, б, мы видим, что
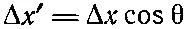 (2.22)
(2.22)
и
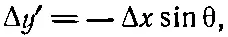 (2.23)
(2.23)
так как Δy отрицательно при положительном Δx. Подставляя в (2.21), получаем
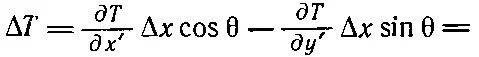 (2.24)
(2.24)
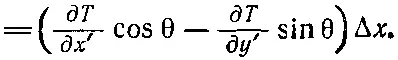 (2.25)
(2.25)
Сравнивая (2.25) с (2.20), мы видим, что
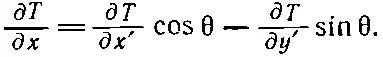 (2.26)
(2.26)
Это уравнение говорит нам, что ∂ T /∂ x получается из ∂ T /∂ x ' и ∂ T /∂ y ' в точности так же, как х из х ' и у ' в (2.18). Значит, ∂ T /∂ x — это x-компонента вектора. Сходные же рассуждения показывают, что ∂ T /∂ y и ∂ T /∂ z суть у - и z-компоненты. Стало быть, ∇ Т есть на самом деле вектор. Это векторное поле, образованное из скалярного поля Т .
А сейчас мы проделаем крайне занятную и остроумную вещь — одну из тех, которые так украшают математику. Доказательство того, что grad Т , или ∇T является вектором, не зависит от того, какое скалярное поле мы дифференцируем. Все доводы остались бы в силе, если бы Т было заменено любым скалярным полем . А поскольку уравнения преобразований одинаковы независимо от того, что дифференцируется, то можно Т убрать и уравнение (2.26) заменить операторным уравнением
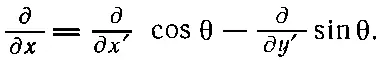 (2.27)
(2.27)
Как выразился Джинс, мы оставляем операторы «жаждущими продифференцировать что угодно».
Так как сами дифференциальные операторы преобразуются как компоненты векторного поля, то можно назвать их компонентами векторного оператора . Можно написать
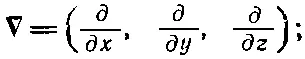 (2.28)
(2.28)
это означает, конечно,
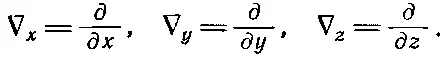 (2.29)
(2.29)
Мы абстрагировали градиент от Т — в этом и есть остроумие.
Конечно, вы должны все время помнить, что ∇— это оператор. Сам по себе он ничего не означает. А если ∇сам по себе ничего не означает, то что выйдет, если мы градиент помножим на скаляр, например на T, чтобы получилось произведение T ∇? (Ведь вектор всегда можно умножить на скаляр.) Это опять ничего не означает. Компонента х этого выражения равна
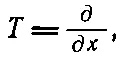 (2.30)
(2.30)
а это не число, а все еще какой-то оператор. Однако в согласии с алгеброй векторов Т ∇по-прежнему можно называть вектором.
А сейчас помножим ∇на скаляр с другой стороны. Получится произведение ∇ T . В обычной алгебре
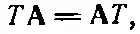 (2.31)
(2.31)
Читать дальше

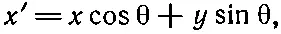 (2.16)
(2.16)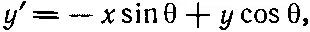 (2.17)
(2.17)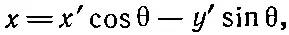 (2.18)
(2.18)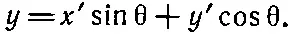 (2.19)
(2.19)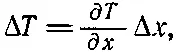 (2.20)
(2.20)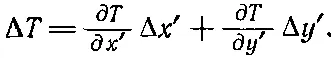 (2.21)
(2.21)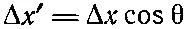 (2.22)
(2.22)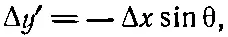 (2.23)
(2.23)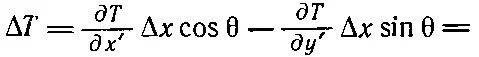 (2.24)
(2.24)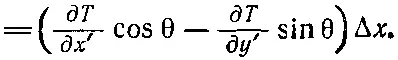 (2.25)
(2.25)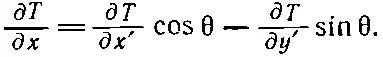 (2.26)
(2.26)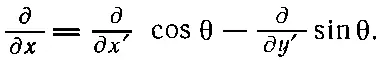 (2.27)
(2.27)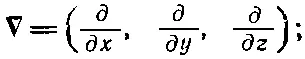 (2.28)
(2.28)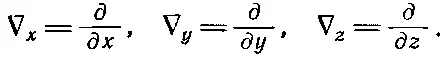 (2.29)
(2.29)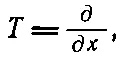 (2.30)
(2.30)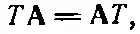 (2.31)
(2.31)



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)


