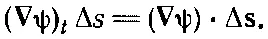 (3.2)
(3.2)
Интеграл в (3.1) и подразумевает сумму таких членов.
А теперь посмотрим, почему уравнение (3.1) правильно. В гл. 1 мы показали, что составляющая ∇ψ вдоль малого смещения Δ Rравна быстроте изменения ψ в направлении Δ R. Рассмотрим хорду кривой Δs от точки (1) до точки а на фиг. 3.2.
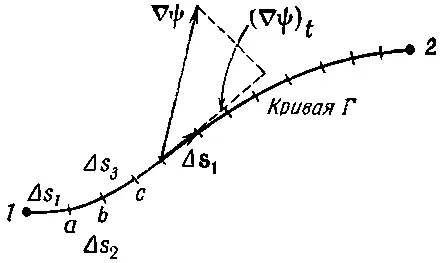
Фиг. 3.2. Криволинейный интеграл есть предел суммы.
По нашему определению
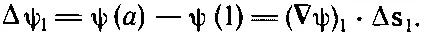 (3.3)
(3.3)
Точно так же мы имеем
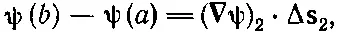 (3.4)
(3.4)
где, конечно, ( ∇ψ) 1означает градиент, вычисленный на хорде Δ s 1, а ( ∇ψ) 2— градиент, вычисленный на Δ s 2. Сложив (3.3) и (3.4), получим
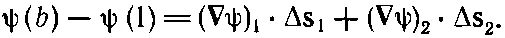 (3.5)
(3.5)
Вы видите, что, продолжая прибавлять такие члены, мы получаем в итоге
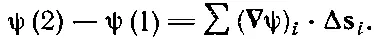 (3.6)
(3.6)
Левая часть не зависит от того, как выбирать интервалы — лишь бы точки (1) и (2) были теми же самыми, так что справа можно перейти к пределу. Так доказывается уравнение (3.1). Из нашего доказательства видно, что, подобно тому как равенство не зависит и от выбора точек а, b, с ,..., точно так же оно не зависит от выбора самой кривой Γ. Теорема верна для любой кривой, соединяющей точки (1) и (2).
Два слова об обозначениях. Не будет путаницы, если писать для удобства
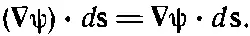 (3.7)
(3.7)
Тогда наша теорема примет такой вид:
ТЕОРЕМА 1
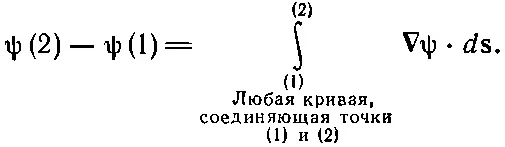 (3.8)
(3.8)
§ 2. Поток векторного поля
Прежде чем рассматривать следующую интегральную теорему — теорему о дивергенции,— хотелось бы разобраться в одной идее, смысл которой в случае теплового потока легко усваивается. Мы уже определили вектор h, представляющий количество тепла, протекающего сквозь единицу площади в единицу времени. Положим, что внутри тела имеется замкнутая поверхность S , ограничивающая объем V (фиг. 3.3). Нам хочется узнать, сколько тепла вытекает из этого объема . Мы это можем, конечно, определить, рассчитав общий тепловой поток через поверхность S .
Обозначим через da площадь элемента поверхности. Этот символ заменяет двумерный дифференциал. Если, например, элемент окажется в плоскости ху , то
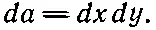
Позже мы будем иметь дело с интегралами по объему, и тогда будет удобно рассматривать элемент объема в виде малого кубика и обозначать его dV , подразумевая, что
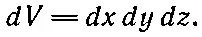
Кое-кто пишет и d 2 a вместо da , чтобы напомнить самому себе, что это выражение второй степени; вместо dV пишут также d 3V. Мы будем пользоваться более простыми обозначениями, а вы уж постарайтесь не забывать, что у площадей бывают два измерения, у объемов — три.
Поток тепла через элемент поверхности da равен произведению площади на составляющую h, перпендикулярную к da . Мы уже определяли n— единичный вектор, направленный наружу перпендикулярно к поверхности (см. фиг. 3.3).
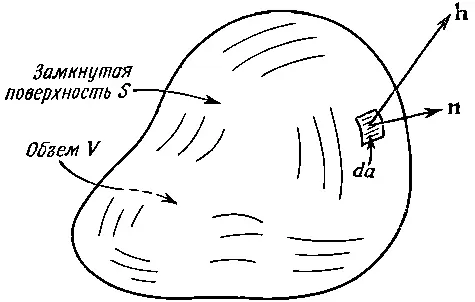
Фиг. 3.3. Замкнутая поверхность S, ограничивающая объем V. Единичный вектор n — внешняя нормаль к элементу поверхности da, а h— вектор теплового потопа сквозь элемент поверхности.
Искомая составляющая hравна
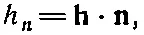 (3.9)
(3.9)
и тогда поток тепла сквозь da равен
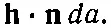 (3.10)
(3.10)
Читать дальше

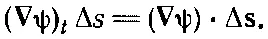 (3.2)
(3.2)
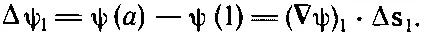 (3.3)
(3.3)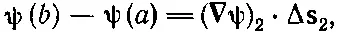 (3.4)
(3.4)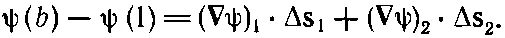 (3.5)
(3.5)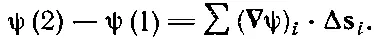 (3.6)
(3.6)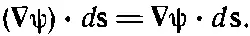 (3.7)
(3.7)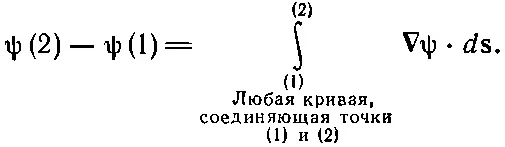 (3.8)
(3.8)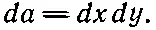
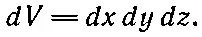

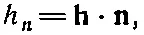 (3.9)
(3.9)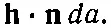 (3.10)
(3.10)



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)


