Все предыдущее рассмотрение было посвящено движению в одном измерении, а теперь мы коротко остановимся на движении в пространстве трех измерений. Рассмотрим движение частицы Р в трехмерном пространстве. Эта глава началась с обсуждения одномерного движения легковой машины, а именно с вопроса, на каком расстоянии от начала движения находится машина в различные моменты времени. Затем мы обсуждали связь между скоростью и изменением расстояния со временем и связь между ускорением и изменением скорости. Давайте в той же последовательности разберем движение в трех измерениях. Проще, однако, начать с более наглядного двумерного случая, а уж потом обобщить его на случай трех измерений. Нарисуем две пересекающиеся под прямым углом линии (оси координат) и будем задавать положение частицы в любой момент времени расстояниями от нее до каждой из осей. Таким образом, положение частицы задается двумя числами (координатами) х и у , каждое из которых является соответственно расстоянием до оси у и до оси х (фиг. 8.3). Теперь мы можем описать движение, составляя, например, таблицу, в которой эти две координаты заданы как функции времени. (Обобщение на трехмерный случай требует введения еще одной оси, перпендикулярной двум первым, и измерения еще одной координаты z . Однако теперь расстояния берутся не до осей, а до координатных плоскостей .) Как определить скорость частицы? Для этого мы сначала найдем составляющие скорости по каждому направлению, или ее компоненты. Горизонтальная составляющая скорости, или x-компонента, будет равна производной по времени от координаты x , т. е.
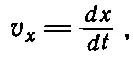 (8.11)
(8.11)
а вертикальная составляющая, или y -компонента, равна
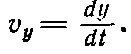 (8.12)
(8.12)
В случае трех измерений необходимо еще добавить
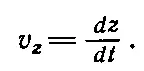 (8.13)
(8.13)
Как, зная компоненты скорости, определить полную скорость в направлении движения? Рассмотрим в двумерном случае два последовательных положения частицы, разделенных коротким интервалом времени Δ t = t 2- t 1и расстоянием Δ s . Из фиг. 8.3 видно, что
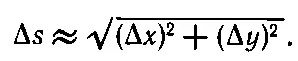 (8.14)
(8.14)
(Значок ≈ соответствует выражению «приблизительно равно».)
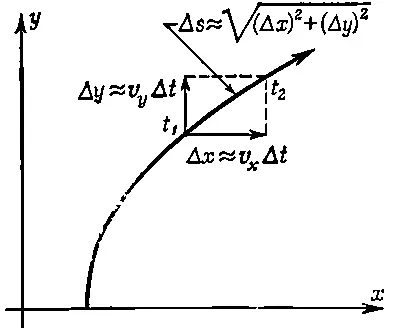
Фиг. 8.3. Описание движения тела на плоскости и вычисление его скорости.
Средняя скорость в течение интервала Δ t получается простым делением: Δ s /Δ t . Чтобы найти точную скорость в момент t , нужно, как это уже делалось в начале главы, устремить Δ t к нулю. В результате оказывается, что
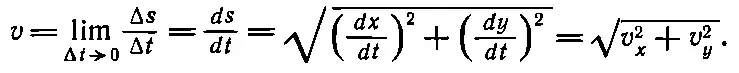 (8.15)
(8.15)
В трехмерном случае точно таким же способом можно получить
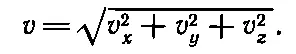 (8.16)
(8.16)
Ускорения мы определяем таким же образом, как и скорости: x -компонента ускорения а х определяется как производная от x-компоненты скорости v x (т. е. a x = d 2 x / dt 2— вторая производная по времени) и т. д.
Давайте рассмотрим еще один интересный пример смешанного движения на плоскости. Пусть шарик движется в горизонтальном направлении с постоянной скоростью u и в то же время падает вертикально вниз с постоянным ускорением g . Что это за движение? Так как v x = dx / dt = u и, следовательно, скорость v x постоянна, то
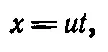 (8.17)
(8.17)
а поскольку ускорение движения вниз постоянно и равно - g , то координата у падающего шара дается формулой
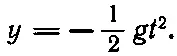 (8.19)
(8.19)
Какую же кривую описывает наш шарик, т. е. какая связь между координатами x и y ? Из уравнения (8.18), согласно (8.17), можно исключить время, поскольку t = x / u , после чего находим
Читать дальше

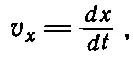 (8.11)
(8.11)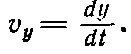 (8.12)
(8.12)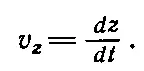 (8.13)
(8.13)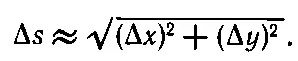 (8.14)
(8.14)
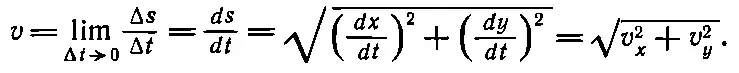 (8.15)
(8.15)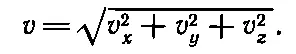 (8.16)
(8.16)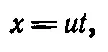 (8.17)
(8.17)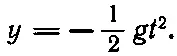 (8.19)
(8.19)




