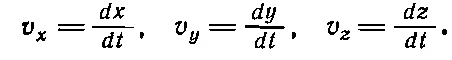 (9.5)
(9.5)
При этом абсолютная величина равна
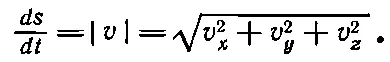 (9.6)
(9.6)
Теперь пусть под действием силы меняется не только величина, но и направление скорости (фиг. 9.2).
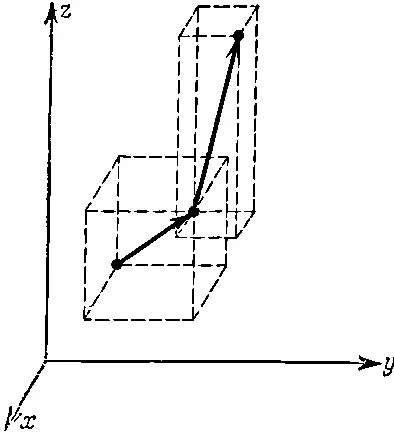
Фиг. 9.2. Скорость изменяется как по величине, так и по направлению.
Хотя это довольно сложный случай, но с помощью подсчета изменения компонент его рассмотрение сильно упрощается. Изменение x -компоненты скорости за интервал Δ t будет Δ v x = a x Δ t , где а хто, что называется x -компонентой ускорения. Совершенно аналогично Δ v x = a y Δ t и Δ v z=a zΔ t . В такой формулировке Второй закон Ньютона фактически превращается в три закона. Действительно, мы говорим, что сила имеет то же направление, что и ускорение, так что каждая из составляющих силы в направлениях x, y и z равна массе, умноженной на изменение соответствующей компоненты скорости:
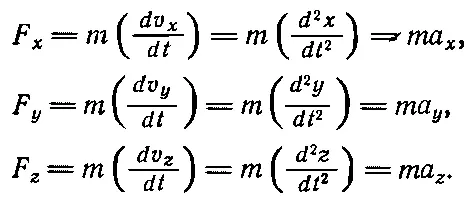 (9.7)
(9.7)
Подобно скорости и ускорению, сила тоже может быть разложена на компоненты, причем каждая из них является проекцией отрезка прямой, численно равного абсолютной величине силы и указывающего направление ее действия, на оси x, y и z :
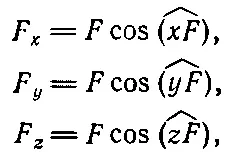 (9.8)
(9.8)
где F — абсолютная величина силы, а ( xF ), ( yF ) и ( zF ) — углы между направлением силы и осями x, y и z соответственно.
Уравнения (9.7) представляют собой полную форму Второго закона Ньютона. Зная силы, действующие на тело, и разлагая их на компоненты, можно с помощью этих уравнений найти движение тела. Давайте рассмотрим простой пример. Пусть в направлениях х и у не действуют никакие силы, а есть сила только в направлении z (скажем, вертикально). Тогда, согласно уравнению (9.7), изменяется только одна вертикальная составляющая скорости; что же касается горизонтальных, то они будут оставаться неизменными. Пример такого движения уже рассматривался в гл. 7 (см. фиг. 7.3). Таким образом, горизонтальное движение падающего тела остается неизменным, тогда как в вертикальном направлении оно движется так, как будто никакого горизонтального движения вообще нет. Другими словами, если компоненты сил не связаны друг с другом, то и движения в направлениях осей x, y и z будут независимы.
Чтобы пользоваться законами Ньютона, мы должны иметь какую-то формулу для сил; ведь эти законы говорят нам: подумайте о силах. Если тело ускоряется, стало быть, на него что-то действует. А как найти это «что-то»? Нашей программой на будущее должно быть отыскание законов для сил. Некоторые из таких законов были найдены самим Ньютоном. Например, формула для силы тяготения. Часть сведений о силах другого рода содержится в Третьем законе, который утверждает равенство сил действия и противодействия, но об этом более подробно пойдет речь в следующей главе.
Продолжим наш предыдущий пример. Что за силы действуют на тело вблизи поверхности Земли? Это — сила тяжести, направленная вертикально вниз, пропорциональная массе тела и для высот, много меньших, чем радиус Земли R , почти не зависящая от высоты; она равна F = GmM / R 2= mg , где g = GM / R 2— так называемое ускорение силы тяжести. В горизонтальном направлении тело по-прежнему будет двигаться с постоянной скоростью, однако движение в вертикальном направлении более интересно. По Второму закону Ньютона
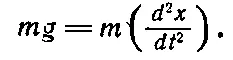 (9.9)
(9.9)
После сокращения массы m получаем, что ускорение в направлении x постоянно и равно g . Это хорошо известное движение свободно падающего тела, которое описывается уравнениями
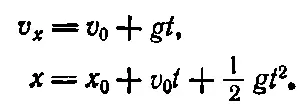 (9.10)
(9.10)
Читать дальше

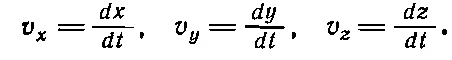 (9.5)
(9.5)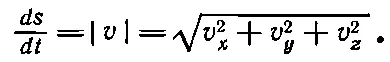 (9.6)
(9.6)
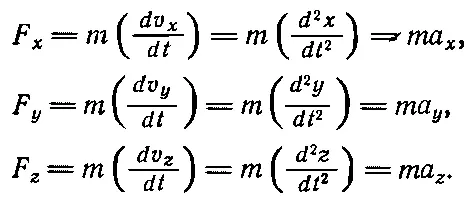 (9.7)
(9.7)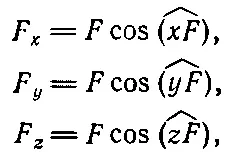 (9.8)
(9.8)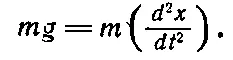 (9.9)
(9.9)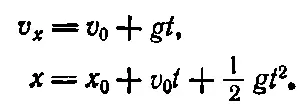 (9.10)
(9.10)




