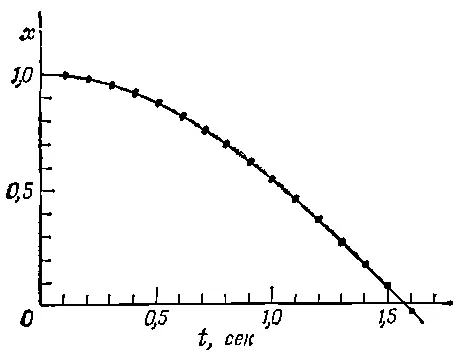
Фиг. 9.4. График движения грузика на пружинке.
Оказывается, что в пределах точности наших расчетов (три знака после запятой) совпадение полное! Позднее вы узнаете, что функция cos t — точное решение нашего уравнения, так что у вас теперь есть наглядное представление о мощи численного анализа: столь простой расчет дает столь точный результат.
Приведенный анализ очень подходит к движению осциллирующей пружинки с грузиком, но можно ли таким же путем вычислять движение планеты вокруг Солнца? Давайте посмотрим, можно ли при некоторых приближениях получить эллиптическую орбиту. Предположим, что Солнце бесконечно тяжелое в том смысле, что его движение не будет приниматься в расчет.
Допустим, что в известной точке планета начала свое движение и имеет определенную скорость. Она движется вокруг Солнца по какой-то кривой, и мы попытаемся определить с помощью уравнений движения Ньютона и его же закона всемирного тяготения, что это за кривая. Как это сделать? В некоторый момент времени планета находится в каком-то определенном месте, на расстоянии r от Солнца; в этом случае известно, что на нее действует сила, направленная по прямой к Солнцу, которая, согласно закону тяготения, равна определенной постоянной, умноженной на произведение масс планеты и Солнца и деленной на квадрат расстояния между ними. Чтобы рассуждать дальше, нужно выяснить, какое ускорение вызывает эта сила.
Однако в отличие от предыдущей задачи нам потребуются теперь компоненты ускорения в двух направлениях, которые мы назовем х и у. Положение планеты в данный момент будет определяться координатами х и у, поскольку третья координата z всегда равна нулю.
Действительно, координатная плоскость xy выбрана нами таким образом, что z -компоненты как силы, так и начальной скорости равны нулю, а поэтому нет никаких причин, которые бы заставили планету выйти из этой плоскости. Сила при этом будет направлена по линии, соединяющей планету с Солнцем, как это показано на фиг. 9.5.
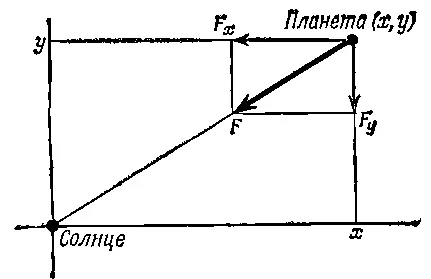
Фиг. 9.5. Сила притяжения, действующая на планету.
Из этого рисунка видно, что горизонтальная компонента силы так относится к полной ее величине, как координата x относится к расстоянию r . Это сразу следует из подобия треугольников. Кроме того, если x положительна, то F x отрицательна, и наоборот.
Таким образом, F x /| F |=- x / r , или F x =-| F | x / r =- GMmx / r 3и соответственно F y =- GMmy / r 3. Теперь можно воспользоваться динамическими законами (9.7) и написать, что x - или y -компонента ускорения, умноженная на массу планеты, равна соответственно x - или y -компоненте силы:
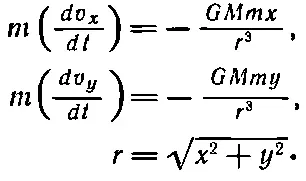 (9.17)
(9.17)
Это именно та система уравнений, которую мы должны решить. Для того чтобы упростить вычисления, предположим, что либо единицы измерения времени или массы выбраны соответствующим образом, либо нам просто повезло, словом, получилось так, что GM ≡1. Для нашего случая предположим, что в начальный момент t =0 планета находилась в точке с координатами x =0,500 и y =0,000, а скорость ее в этот момент направлена параллельно оси y и равна 1,6300. Как же в этом случае делаются расчеты? Снова составляется таблица со столбцами для времени t , координаты x, x -компонент скорости v x и ускорения a x . Затем идут отделенные чертой три колонки: для координаты y, y -компонент скорости и ускорения. Однако, для того чтобы подсчитать ускорения, мы должны воспользоваться уравнением (9.17), согласно которому его компоненты равны — x / r 3и — y / r 3, а r =√( x 2+ y 2). Так что, получив x и y , мы должны где-то в сторонке провести небольшие вычисления — извлечь квадратный корень из суммы квадратов и получить расстояние. Удобно также отдельно вычислить и 1/ r 3.
После этого все готово, чтобы определить компоненты ускорения. Всю эту работу можно сильно облегчить, если пользоваться таблицами квадратов, кубов и обратных величин. На нашу долю останется тогда только умножение x на 1/ r 3, которое легко выполняется на логарифмической линейке.
Читать дальше



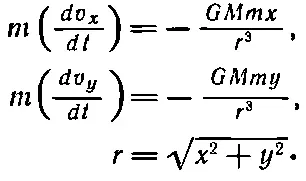 (9.17)
(9.17)




