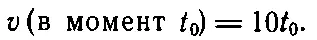т. е. скорость есть предел отношения х /ε при ε, стремящемся к нулю. Для нашей машины-нарушительницы невозможно точно вычислить скорость, так как таблица неполная. Ее положение известно нам только через интервалы 1 мин . Приближенно, конечно, можно сказать, что в течение седьмой минуты, например, она шла со средней скоростью 90 км / час , однако о ее скорости в конце шестой минуты ничего сказать невозможно. Может быть, она ускорялась и скорость с 40 км / час в начале шестой минуты возросла до 90 км / час в конце ее, а может быть, она двигалась иначе. Мы не знаем этого точно, так как у нас нет детальной записи ее движения между шестой и седьмой минутами. Только когда таблица будет пополнена бесконечным числом данных, из нее можно будет действительно вычислить скорость. Если, однако, нам известна полная математическая формула, как, например, в случае падающего тела [уравнение (8.1)], то можно подсчитать скорость. Ведь по формуле можно найти положение тела в любой момент времени.
В качестве примера давайте найдем скорость падающего шара через 5 сек после начала падения. Один способ — это посмотреть по табл. 8.2, что происходило с шариком на пятой секунде. В течение этой секунды он прошел 45 м , так что, казалось бы, он падал со скоростью 45 м / сек . Однако это неверно, поскольку скорость его все время изменялась. Конечно, в среднем в течение этой секунды она составляла 45 м / сек , но в действительности шар ускорялся и в конце пятой секунды падал быстрее 45 м / сек . Наша задача состоит в том, чтобы определить скорость точно . Сделаем это следующим образом. Нам известно, где шарик находился через 5 сек . За 5 сек он прошел расстояние 125 м . К моменту 5,1 сек общее расстояние, которое прошел шарик, составит, согласно уравнению (8.1), 130,05 м . Таким образом, за дополнительную десятую долю секунды он проходит 5,05 м . А поскольку 5,05 м за 0,1 сек то же самое, что и 50,5 м / сек , то это и будет его скорость. Однако это все еще не совсем точно. Для нас совершенно неважно, будет ли это скорость в момент 5 сек , или в момент 5,1 сек , или где-то посредине. Наша задача вычислить скорость точно через 5 сек , а этого мы пока не сделали. Придется улучшить точность и взять теперь на тысячную долю больше 5 сек , т. е. момент 5,001 сек . Полное расстояние, пройденное за это время, составляет
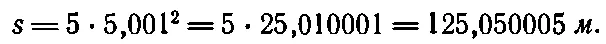
Следовательно, в последнюю тысячную долю секунды шарик проходит 0,050005 м , и если разделить это число на 0,001 сек , то получим скорость 50,005 м / сек . Это уже очень близко, но все же еще не точно . Однако теперь уже ясно, как поступить, чтобы найти скорость точно. Удобнее решать эту задачу в несколько более общем виде. Пусть требуется найти скорость в некоторый момент времени t 0(например, 5 сек ). Расстояние, которое пройдено к моменту t 0(назовем его s 0), будет 5 t 0 2(в нашем случае 125 м ). Чтобы определить расстояние, мы задавали вопрос: где окажется тело спустя время t 0+(небольшой добавок), или t 0+ε? Новое положение тела будет 5( t 0+ε) 2=5 t 2 0+10 t 0ε+5ε 2. (Это расстояние больше того расстояния, которое шарик прошел за t 0 сек, т. е . больше 5 t 0 2). Назовем это расстояние s 0+(небольшой добавок), или s 0+ x . Если теперь вычесть из него расстояние, пройденное к моменту t 0, то получим х — то дополнительное расстояние, которое шарик прошел за добавочное время ε, т. е. x=10t 0ε+5ε 2. Так что в первом приближении скорость будет равна
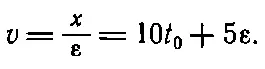 (8.4)
(8.4)
Теперь мы уже знаем, что нужно делать, чтобы получить скорость точно в момент t 0: нужно брать отрезок ε все меньше и меньше, т. е. устремлять его к нулю. Таким путем из уравнения (8.4) получим
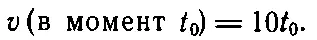
В нашей задаче t 0=5 сек , следовательно, скорость равна у=10·5=50 м / сек . Это и есть нужный ответ. Раньше, когда ε бралось равным 0,1 и 0,001 сек, получалась несколько большая величина, чем 50 м / сек , но теперь мы видим, что в действительности она в точности равна 50 м / сек .
Читать дальше

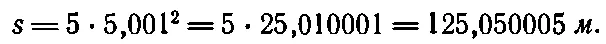
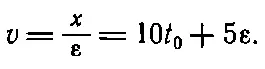 (8.4)
(8.4)