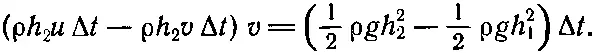Ричард Фейнман - Том 1. Механика, излучение и теплота

Фиг. 51.4. Падение воды и водовороты.

Можно показать, что длинные волны в канале идут быстрее по глубокой воде, чем по мелкой. Поэтому любой новый толчок или какие-то иные нерегулярности в энергии, поступающей от поршня, побегут вперед и соберутся на фронте волны. Теоретически мы снова в конце концов должны получить резкий фронт. Однако (см. фиг. 51.4) здесь возникают некоторые усложнения. Вы видите волну, идущую вверх по каналу, причем поршень находится где-то далеко с правой стороны канала. Сначала может показаться, что это хорошая волна, такая, какую и следует ожидать, но дальше она становится острее и острее, пока не произойдет то, что изображено на рисунке. Вода на поверхности начинает сильно бурлить и переливаться вниз, но, что самое существенное, край по-прежнему остается резким, и впереди него нет никакого возмущения.

В действительности волна на воде — вещь куда более сложная, чем звук. Однако для иллюстрации мы попытаемся проанализировать скорость так называемого высокого прилива в канале . Дело не в том, что это очень важно для наших целей (никакого обобщения здесь не будет), это только иллюстрация того, как законы механики, которые мы хорошо знаем, способны объяснить подобное явление.

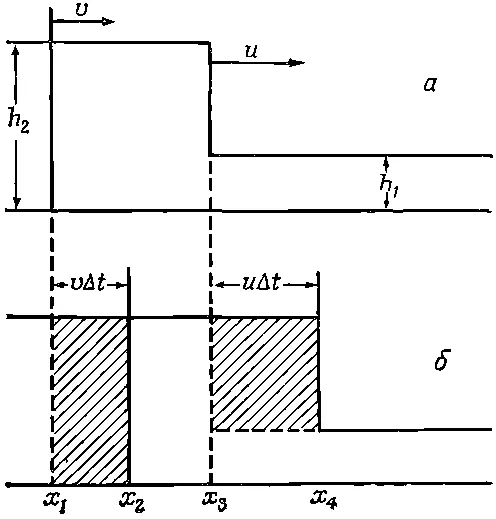
Фиг. 51.5. Два разреза высокого прилива в канале. Разрез б сделан на интервал времени Δt позднее разреза а.

Вообразите на минуту, что поверхность воды имеет такой вид, как изображено на фиг. 51.5,а, и что на верхнем уровне h 2она движется со скоростью v , а фронт со скоростью u надвигается на невозмущенную поверхность, высота которой h 1. Мы хотим определить скорость, с которой движется фронт. За промежуток времени Δ t вертикальная плоскость, проходившая вначале через точку x 1передвинется на расстояние v Δ t , т. е. от х 1до х 2, а фронт волны пройдет расстояние u Δ t .

Применим теперь законы сохранения вещества и импульса. Возьмем сначала первый из них: мы видим, что на единицу ширины канала количество вещества h 2 v Δ t , прошедшее мимо точки x 1(область, заштрихованная на фиг. 51.5,б), компенсируется другой заштрихованной областью, представляющей количество вещества (h 2- h 1) u Δ t . Разделив на Δ t , получим vh 2= u ( h 2- h 1). Но этого еще недостаточно, так как, хотя нам известны h 1и h 2, мы еще не знаем ни u , ни v , а хотим найти обе величины.

Следующим шагом будет использование закона сохранения импульса. Мы еще не касались вопросов давления в воде и прочей гидродинамики, но и так ясно, что давление в воде на какой-то глубине должно быть как раз достаточным, чтобы поддерживать столбик воды над этой глубиной. Следовательно, давление воды равно произведению плотности ρ на g и на глубину. Так как давление воды возрастает линейно с глубиной, то среднее давление на плоскость, проходящую, например, через точку х 1, равно 1/ 2ρ gh 2, что также представляет среднюю силу на единичную ширину и на единичную длину, толкающую плоскость к точке х 2. Чтобы получить полную силу, давящую на воду слева, мы должны еще раз умножить на h 2. С другой стороны, давление на рассматриваемую область справа дает противоположно направленную силу, которая по тем же причинам равна 1/ 2ρ gh 1 2. Теперь мы должны приравнять эти силы к скорости изменения импульса. Таким образом, нам нужно выяснить, насколько в случае, изображенном на фиг. 51.5,6, импульс больше, чем в случае, показанном на фиг. 51.5,а.

Мы видим, что дополнительная масса, которая приобрела скорость v равна просто ρh 2uΔt—ρh 2vΔt (на единицу ширины), а умножение ее на v дает дополнительный импульс, который должен быть приравнен к импульсу силы F Δ t :

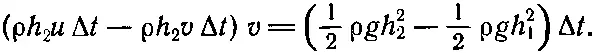
Исключая из этого уравнения v подстановкой vh 2= u ( h 2- h 1) и упрощая его, получаем окончательно u 2= gh 2( h 1+ h 2)/2 h 1.

Если разность высот очень мала, так что h 1и h 2приблизительно одинаковы, то скорость будет равна √( gh ). Как мы увидим позднее, это справедливо только при условии, что длина волны много больше глубины канала.