Любое движение можно рассматривать как составленное из различных собственных гармоник, взятых с надлежащими амплитудами и фазами .
Значение этого принципа обусловлено тем фактом, что каждое собственное колебание — очень простая вещь — это просто синусоидальное движение во времени. По правде говоря, даже общее движение струны — еще не самая сложная вещь; существует движение куда более сложное, скажем такое, как вибрация крыльев самолета. Тем не менее даже у крыльев самолета можно обнаружить некие собственные кручения с определенными частотами. А если так, то полное движение можно рассматривать как суперпозицию гармонических колебаний (за исключением тех случаев, когда вибрация настолько велика, что система уже не может рассматриваться как линейная).
§ 3. Двумерные собственные колебания
Сейчас мы перейдем к рассмотрению очень интересного поведения собственных гармоник в двумерных колебаниях. До сих пор мы говорили только об одномерных колебаниях: натянутой струне или звуковых волнах в трубе. В конце концов мы должны добраться до трех измерений, но сначала давайте остановимся на более легком этапе — этапе двумерных колебаний. Возьмем для большей определенности прямоугольный резиновый барабан, перепонка которого закреплена по краям так, что на прямоугольном крае барабана она перемещаться не может. Пусть размеры прямоугольника будут равны а и b , как это показано на фиг. 49.4.
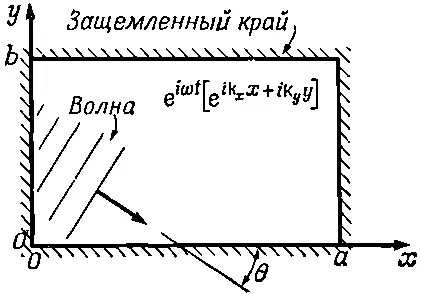
Фиг. 49.4. Колебание прямоугольной пластинки.
Прежде всего, каковы характеристики возможного движения? Можно начать с того же, с чего мы начали, когда рассматривали пример со струной. Если бы никакого закрепления не было вовсе, то можно было бы ожидать появления волн, бегущих в некотором направлении, например синусоидальной волны, описываемой функцией ехр ( i ω t ) ехр [- i ( k x x )+i( k y y )], направление движения которой зависит от относительной величины чисел k x и k y . А как теперь сделать узел на оси х , т. е. при y=0? Используя ту же идею, что и для одномерной струны, можно добавить волну, описываемую комплексной функцией - exp ( i ω t ) ехр [- i ( k x x )-i( k y y )].
Суперпозиция этих волн в результате дает нулевое перемещение при y=0 независимо от того, каковы будут значения х и t . (Хотя эти функции будут определены и для отрицательных значений у там, где никакого барабана нет и колебаться нечему, но на это можно не обращать никакого внимания. Ведь нам хотелось устранить перемещение при у =0, и мы добились этого.) Вторую функцию в этом случае можно рассматривать как отраженную волну.
Однако нам нужно получить узел не только на линии y=0, но и на линии у = b . Как же это сделать? Решение такой задачи связано с некоторыми вещами, которыми мы занимались при изучении отражения света от кристалла. Волны, гасящие друг друга при y=0, могут сделать то же самое и при у = b , только когда 2 b sinθ равно целому числу длин волн λ, (θ — угол, показанный на фиг. 49.4):
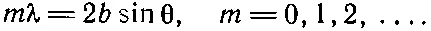 (49.7)
(49.7)
Точно таким же образом, т.е. сложением еще двух функций [-exp( i ω t )] exp [ i ( k x x )+ i ( k y y )] и [+ exp ( i χ t )] exp [ i ( k x x )- i ( k y y )], каждая из которых представляет отражение другой от линии х =0, можно устроить узел и на оси у . Условие того, что линия х = а будет тоже узловой, получается так же, как и условие при у = b , т. е. 2acosθ должно быть равно целому числу длин волн:
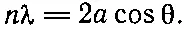 (49.8)
(49.8)
Тогда окончательный результат таков: волны, «заключенные» в ящике, имеют вид стоячей волны, т. е. образуют какие-то определенные собственные гармоники.
Таким образом, если мы хотим иметь дело с собственными гармониками, то должны удовлетворить двум написанным выше условиям. Для начала давайте найдем длину волны. Исключив из уравнений (49.7) и (49.8) угол θ, можно выразить длину волны через a, b, n и m . Легче всего это сделать так: сначала разделить обе части уравнений соответственно на 2 b и 2 a , а затем возвести их в квадрат и сложить. В результате мы получим уравнение
Читать дальше


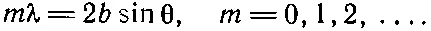 (49.7)
(49.7)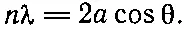 (49.8)
(49.8)




