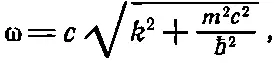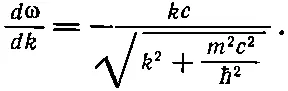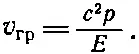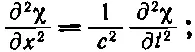т. е. р μ р μ= m 2. Это величайший результат четырехмерья, о котором мы уже говорили много раз, устанавливающий связь между энергией и импульсом в классической теории. Теперь же, поскольку мы собираемся заменить E и p на ω и k помощью подстановки Е = ℏ ω и p =ℏ k , он означает, что в квантовой механике должна существовать связь
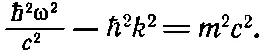 (48.22)
(48.22)
Таким образом, возникло соотношение между частотой и волновым числом квантовомеханической амплитуды, описывающей частицу с массой m . Из этого уравнения можно получить
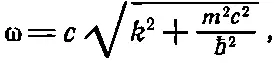
т. е. фазовая скорость ω/k снова больше скорости света!
Рассмотрим теперь групповую скорость. Она должна быть равна скорости, с которой движется модуляция, т. е. d ω/ dk .
Чтобы найти ее, нужно продифференцировать квадратный корень; это дело нехитрое. Производная равна
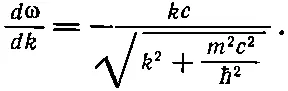
Но входящий сюда квадратный корень есть попросту ω/ с , так что эту формулу можно записать в виде dω/dk=c 2k/ω. Далее, так как k/ω равно р / Е , то
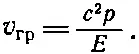
Но, согласно (48.20) и (48.21), с 2 р / Е равно v — скорости частицы в классической механике. Таким образом видно, что, принимая во внимание основные квантовомеханические соотношения E = ℏ ω и p =ℏ k , определяющие ω и k через классические величины Е и р и дающие только уравнение ω 2- k 2 c 2== m 2 с 4/ℏ 2, теперь можно понять также соотношения (48.20) и (48.21), связывающие Е и р со скоростью. Групповая скорость, разумеется, должна быть скоростью частиц, если эта интерпретация вообще имеет какой-либо смысл. Пусть в какой-то момент, как мы полагаем, частица находится в одном месте, а затем, скажем через 10 минут,— в другом. Тогда, согласно квантовой механике, расстояние, пройденное «колоколом», разделенное на интервал времени, должно равняться классической скорости частицы.
§ 6. Волны в пространстве трех измерений
Мы заканчиваем наше обсуждение волн несколькими общими замечаниями о волновом уравнении. Эти замечания, призванные дать нам картину того, чем нам предстоит заниматься в будущем, вовсе не претендуют на то, чтобы вы поняли их сразу; они должны скорее показать, как будут выглядеть все эти вещи, когда вы несколько больше познакомитесь с волнами. Мы уже записали уравнение для распространения звука в одном измерении:
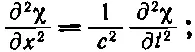
здесь с — скорость того, что мы назвали волнами. Если речь идет о звуке, то это скорость звука, если о свете — то это скорость света. Мы показали, что для звуковой волны перемещения частиц должны распространяться с некоторой скоростью. Но избыточное давление, как и избыточная плотность, тоже распространяется с некоторой скоростью. Таким образом, можно ожидать, что и давление будет удовлетворять этому же уравнению.
Так оно и есть на самом деле, однако докажите это самостоятельно. Указание : ρ u пропорционально скорости изменения χ с расстоянием х . Следовательно, продифференцировав волновое уравнение по х , мы немедленно обнаружим, что ∂χ/∂ x удовлетворяет тому же самому уравнению. Другими словами, ρ uудовлетворяет тому же самому уравнению. Но Р u пропорционально ρ u, поэтому и Р u удовлетворяет тому же самому уравнению. Таким образом, и давление, и перемещение — все описывается одним и тем же уравнением.
Обычно волновое уравнение для звука записывается через давление, а не через перемещение. Это проще, потому что давление — скаляр и не имеет никакого направления. Но перемещение есть вектор, и поэтому лучше иметь дело с давлением.
Следующий вопрос, который нам предстоит обсудить, относится к волновому уравнению в трехмерном пространстве. Мы знаем, что звуковая волна в одномерном пространстве описывается решением ехр[i(ωt- kx )], где ω=kc s. Кроме того, нам известно, что в трех измерениях волна описывается выражением exp[i(ωt- k x x - k y y - k z z )], и в этом случае ω 2=k 2с s 2[сокращенная запись (k x 2+k y 2+k z 2)c S 2]. Сейчас мы хотим просто угадать вид волнового уравнения в трехмерном пространстве. Естественно, что в случае звука это уравнение можно получить с помощью тех же самых динамических соображений, но уже в трехмерном пространстве. Однако мы не будем сейчас делать этого, а просто напишем ответ: уравнение для давления или перемещения (или чего-то другого) имеет вид
Читать дальше

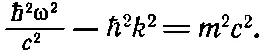 (48.22)
(48.22)