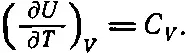 (45.4)
(45.4)
Теперь снова подведем к газу тепло Δ Q , но на этот раз договоримся, что температура газа останется постоянной, а объему мы позволим измениться на ΔV. В этом случае анализ сложнее, но мы можем вычислить ΔU, используя аргументы Карно, для чего нам придется снова призвать на помощь цикл Карно из предыдущей главы.
Диаграмма давление — объем для цикла Карно изображена на фиг. 45.1. Мы уже показали, что полная работа, совершаемая газом при обратимом цикле, равна Δ Q (Δ T / T ), где ΔQ — тепло, подводимое к газу при температуре Т во время изотермического расширения от V до V+ΔV, а Т —Δ Т — это конечная температура, которой достигает газ при адиабатическом расширении на втором этапе цикла. Сейчас мы покажем, что эта работа равна, кроме того, заштрихованной площади на фиг. 45.1. Работа газа во всех случаях жизни равна ∫ PdV ; она положительна, если газ расширяется, и отрицательна, когда он сжимается. Если вычертить зависимость Р от V, то изменения Р и V изобразятся кривой, в каждой точке которой определенному значению Р соответствует определенное значение V. Работа, произведенная газом, пока его объем изменяется от одного значения до другого (интеграл ∫ PdV ),— это площадь под кривой, соединяющей начальное и конечное значения V. Применим эту идею к циклу Карно и убедимся, что если обойти цикл, помня о знаке совершенной газом работы, то чистая работа газа будет равна заштрихованной на фиг. 45.1 площади.
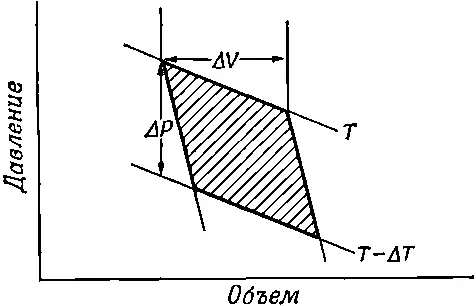
Фиг. 45.1. Диаграмма Р — V для цикла Карно. Кривые, помеченные Т и Т—ΔТ,— изотермы; крутые кривые между ними — адиабаты. Когда газ изотермически расширяется при температуре Т, он получает тепло ΔQ и увеличивает свой объем на ΔV; ΔР—изменение давления при постоянном объеме, температура в это время падает с Т до Т—ΔT.
А теперь вычислим эту площадь чисто геометрически. Цикл, который был использован для получения фиг. 45.1, отличается от цикла, описанного в предыдущей главе тем, что теперь ΔQ и ΔT бесконечно малы. Наши адиабаты и изотермы очень близки друг к другу, поэтому фигура, описанная жирными линиями на фиг. 45.1, приближается к параллелограмму, когда приращения ΔQ и Δ Т стремятся к нулю. Площадь этого параллелограмма в точности равна ΔVΔP (где ΔV — изменение объема, когда к газу подводится энергия Δ Q при постоянной температуре, а ΔР — изменение давления при изменении температуры на ΔT и постоянном объеме). Легко показать, что заштрихованная площадь на фиг. 45.1 равна площади, ограниченной пунктиром на фиг. 45.2.
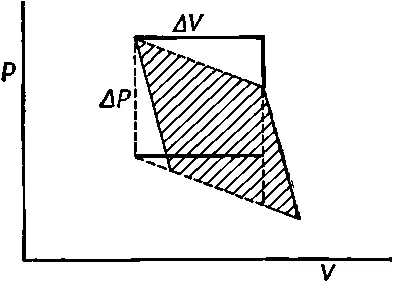
Фиг. 45.2. Заштрихованная площадь=Площадь, ограниченная пунктирными линиями=Площадь прямоугольника=ΔPΔV.
А эту фигуру легко превратить в прямоугольник со сторонами Δ Р и ΔV, для чего нужно лишь вырезать из нее треугольники и сложить их немного иначе.
Соберем все наши выводы вместе.

Выражение (45.5) содержит в себе суть результатов, следующих из аргументов Карно. Всю термодинамику можно вывести из (45.5) и первого закона, содержащегося в уравнении (45.3). Выражение (45.5)— это, в сущности, второй закон, хотя впервые Карно сформулировал его несколько иначе, поскольку не пользовался нашим определением температуры.
А теперь можно приступить к вычислению (∂ U /∂ V ) T . Насколько изменится внутренняя энергия U , если объем изменится на ΔV? Во-первых, внутренняя энергия U меняется за счет подводимого тепла и, во-вторых, за счет совершаемой работы. Подводимое тепло, согласно (45.5), равно
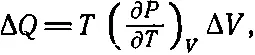
а совершаемая над веществом работа равна —PΔV. Поэтому изменение Δ U складывается из двух кусков
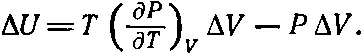 (45.6)
(45.6)
Поделив обе стороны на ΔV, мы найдем скорость изменения U относительно V при постоянной Т
Читать дальше

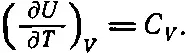 (45.4)
(45.4)


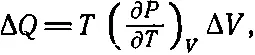
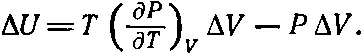 (45.6)
(45.6)




