Коэффициент полезного действия не может быть больше единицы, а абсолютная температура не может быть меньше нуля, абсолютного нуля. Таким образом, раз T 2должна быть положительной, то коэффициент полезного действия всегда меньше единицы. Это наш первый вывод.
Уравнение (44.7) или (44.12) может быть истолковано особо. При работе обратимых машин Q 1/ T 1= Q 2/ T 2, и тепло Q 1при температуре Т 1«эквивалентно» теплу Q 2при температуре T 2; ведь если поглощается Q 1, то всегда выделяется тепло Q 2. Если теперь придумать для Q / T особое название, то можно сказать, что при обратимых процессах поглощается столько же Q / T , сколько и выделяется. Иначе говоря, Q / T не убывает и не прибывает. Эта величина Q / T называется энтропией , и мы говорим, что «за обратимый цикл изменение энтропии равно нулю». Если T=1°, то энтропия равна Q/1°; мы уже снабдили энтропию особым символом S = Q S /1°. Энтропия повсюду обозначается буквой S , а численно она равна теплу (которое мы обозначили буквой Q S ), выделяемому в одноградусном резервуаре (энтропия не равна просто теплу, это тепло, деленное на температуру, и измеряется она в джоулях на градус ).
Интересно, что, кроме давления, которое зависит от температуры и объема, и внутренней энергии (функции все тех же объема и температуры), мы нашли еще величину — энтропию вещества, которая тоже является функцией состояния. Постараемся объяснить, как вычислять энтропию и что мы понимаем под словами «функция состояния». Проследим за поведением системы в разных условиях. Мы уже умеем создавать разные условия экспериментально, например можно заставить систему расширяться адиабатически или изотермически. (Между прочим, машина не обязательно должна иметь только два резервуара, может быть и три, и четыре различные температуры, и машина будет обмениваться теплом с каждым из резервуаров.) Мы можем прогуляться по всей диаграмме pV , переходя от одного состояния к другому. Иначе говоря, можно перевести газ из состояния а в какое-нибудь другое состояние b и потребовать, чтобы переход из а в b был обратимым. Теперь предположим, что вдоль пути из а в b поставлены маленькие резервуары с разными температурами. Тогда каждый короткий шажок будет сопровождаться изъятием из вещества тепла dQ и передачей его в резервуар при температуре, соответствующей данной точке пути. Давайте свяжем все эти резервуары с помощью обратимых тепловых машин с одним резервуаром единичной температуры. После того как мы закончим перевод вещества из состояния а в состояние b , мы вернем все резервуары в их первоначальное состояние. Обратимая машина вернет каждую дольку тепла dQ , изъятого из вещества при температуре Т , и каждый раз при единичной температуре будет выделяться энтропия dS , равная
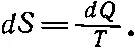 (44.15)
(44.15)
Подсчитаем полное количество выделенной энтропии. Разность энтропии, или энтропия, нужная для перехода из а в b в результате какого-нибудь обратимого изменения, это — полная энтропия, т. е. энтропия, взятая из маленьких резервуаров и выделенная при единичной температуре:
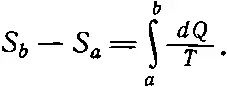 (44.16)
(44.16)
Вопрос заключается в том, зависит ли разность энтропии от пути в плоскости pV? Из а в b ведет много дорог. Вспомним, что в цикле Карно мы могли перейти из точки а в точку с (см. фиг. 44.6) двумя способами. Можно было расширить газ сначала изотермически, а потом адиабатически, а можно было начать с адиабатического расширения и окончить изотермическим. Итак, мы должны выяснить, меняется ли энтропия при изменении пути из а в b (фиг. 44.10).
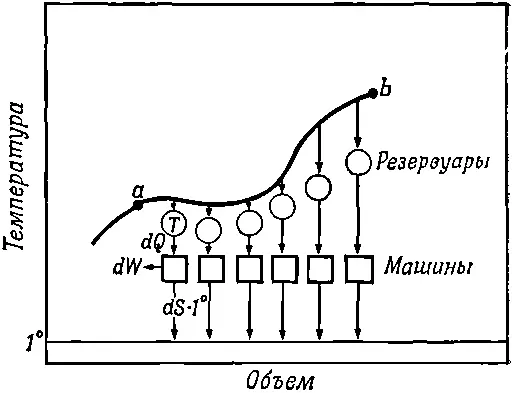
Фиг. 44.10. Изменение энтропии при обратимом переходе.
Она не должна измениться , потому что если мы совершим полный цикл, выйдя из а в b по одному пути и возвратясь по другому, то это путешествие будет эквивалентно полному циклу обратимой машины. При таком цикле никакого тепла не передается одноградусному резервуару.
Читать дальше

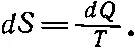 (44.15)
(44.15)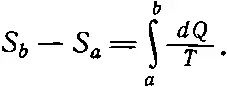 (44.16)
(44.16)





