Ричард Фейнман - Том 1. Механика, излучение и теплота

Чтобы загнать атомы в состояние m , прибегают к разным ухищрениям. Может существовать более высокий уровень, на который атомы можно поднять сильным пучком света высокой частоты. С этого высокого уровня атомы падают вниз, испуская самые различные фотоны, пока не соберутся на уровне m . Если атомы стремятся задержаться на уровне m , не излучая фотонов, то этот уровень называют метастабильным . А потом атомы разом спрыгивают с уровня m , сопровождая прыжок вынужденным излучением. Еще одна техническая деталь — если поместить нашу систему в обычный ящик, то она может спонтанно излучать во многих направлениях, что наносит ущерб вынужденному излучению. Но можно усилить эффект вынуждения и увеличить его значение, поставив у каждой стенки ящика почти полностью отражающие зеркала; тогда излученный свет получает шанс вызвать дополнительное излучение, следующее отражение добавит еще один такой шанс, а потом еще, еще и еще. Хотя зеркала отражают почти весь свет, существует небольшая вероятность прохождения части света сквозь зеркало и выхода наружу. В конце концов весь свет, подчиняясь закону сохранения энергии, выйдет наружу в виде тонкого, сильного пучка. Так и получают мощные пучки света в лазерах

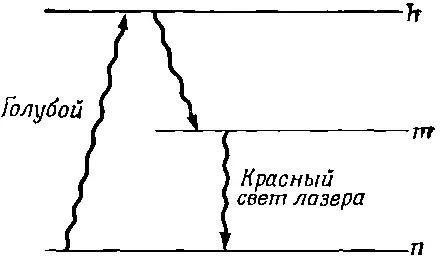
Фиг. 42.3. При возбуждении голубым светом атом поднимается на высший уровень h и, быстро испустив фотон, сваливается с него на уровень m. Когда число атомов в состоянии m становится достаточно большим, возникает действие лазера.

До сих пор мы изучали движение молекул только при тепловом равновесии. А теперь нужно обсудить, как движутся молекулы газа, когда он близок к равновесию, но еще не достиг его полностью. Если газ слишком неравновесен, все становится чрезвычайно сложным и разобраться в том, что там происходит, очень трудно, а вот если отклонения от равновесия незначительны, то задачи решаются легко. Однако, чтобы рассмотреть, что происходит в таком газе, надо снова вернуться к кинетической теории. Статистическая механика и термодинамика пригодны, когда имеется равновесие, а чтобы проанализировать то, что происходит при отклонении от равновесия, приходится, так сказать, перебирать атом за атомом.

В качестве простого примера неравновесной задачи рассмотрим диффузию ионов в газе. Предположим, что в газе содержится немного ионов — электрически заряженных молекул. Если к газу приложить электрическое поле, то на каждый ион будет действовать сила, отличающаяся от сил, действующих на нейтральные молекулы. Если бы других молекул не было, то ион двигался бы с постоянным ускорением, пока не наткнулся бы на стенку ящика. Но наличие других молекул меняет дело: скорость иона возрастает лишь до тех пор, пока он не ударится о молекулу и не потеряет своего импульса. После этого он снова начинает ускоряться, но вновь теряет импульс. В результате ион вынужден двигаться по ломаному пути, хотя все же в конце концов он движется в направлении электрического поля. Мы замечаем, таким образом, что ион «дрейфует» со средней скоростью, пропорциональной электрическому полю; чем сильнее поле, тем быстрее движется ион. Конечно, пока существует поле и пока ион продолжает двигаться, не может быть и речи о тепловом равновесии. Система стремится прийти к равновесию, но для этого нужно, чтобы все ионы приклеились к стенке ящика. С помощью кинетической теории возможно вычислить скорость дрейфа ионов.

Наших математических познаний еще недостаточно, чтобы точно вычислить все, что произойдет, но мы можем получить приближенное решение, которое правильно передаст все существенные особенности явления. Мы можем определить зависимость эффекта от давления, температуры и т. п., но не в наших силах вычислить точно все коэффициенты, стоящие перед этими сомножителями. Поэтому не будем мучить себя заботой о точных значениях таких коэффициентов. Получить их можно только после очень тонкого математического анализа.

Прежде чем рассуждать о том, что происходит в отсутствие равновесия, посмотрим повнимательнее на равновесный газ. Необходимо, например, знать среднее время между двумя последовательными столкновениями молекулы.