Теперь надо найти скорость обратного процесса R r . Есть некоторая вероятность, что А и В снова разойдутся. Чтобы разойтись, им недостаточно энергии W , которая обеспечит их раздельное существование. Но раз молекулам нелегко соединиться, должен существовать некий барьер, через который А и В должны перевалить, чтобы разлететься. Они должны запастись не только нужной для их существования энергией, но и взять кое-что про запас. Получается что-то вроде подъема на холм перед спуском в долину; сначала приходится вскарабкаться на высоту, потом спуститься, и только после этого разойтись (фиг. 42.1).
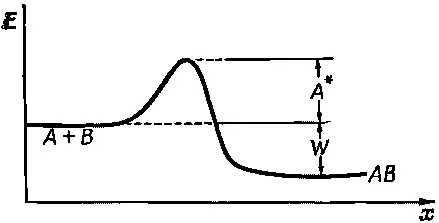
Фиг. 42.1. Соотношение энергий в реакции А+В→АВ.
Таким образом, скорость перехода АВ в А и В пропорциональна произведению n АВ — начальному числу молекул АВ на ехр[-( W + A *)/ kT ]:
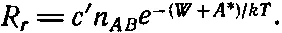 (42.11)
(42.11)
Постоянная с' складывается из объема атомов и частоты столкновений; ее можно получить, как и в случае испарения, перемножая площадь и толщину слоя, но сейчас мы этого делать не будем. Сейчас нас больше интересует тот факт, что, когда эти скорости равны, их отношение равно единице. Это говорит о том, что, как и раньше, ( n A n B / n AB )= c ехр(- W / kT ), где с содержит сечения, скорости и другие множители, не зависящие от чисел n . Интересно, что скорость реакции по-прежнему изменяется как ехр(-const/ kT ), хотя эта постоянная уже не имеет никакого отношения к той, с которой мы встречались в задаче о концентрациях; энергия активации А *сильно отличается от энергии W. Энергия W регулирует пропорции А, В и АВ, при которых устанавливается равновесие , но если нам захочется узнать, быстро ли А + В переходит в АВ , то это уже к равновесию отношения не имеет, и появляется уже другая энергия, энергия активации , которая с помощью экспоненты управляет скоростью реакции.
Кроме того, A *не является фундаментальной постоянной, как W . Предположим, что реакция происходит на поверхности стены, или на какой-нибудь другой поверхности, тогда А и В могут растечься по ней так, что объединение в АВ будет для них более легким делом. Иначе говоря, сквозь гору можно прорыть «туннель» или срыть вершину горы. В силу сохранения энергии, по какому бы пути мы ни шли, результат будет один: из А и В получится АВ , так что разность энергий W не зависит от пути, по которому идет реакция, однако энергия активации А * очень сильно зависит от этого пути. Вот почему скорости химических реакций столь чувствительны к внешним условиям. Можно изменить скорость реакции, изменив поверхность, с которой соприкасаются реактивы, можно изготовить «набор бочонков» и подбирать с его помощью любые скорости, если они зависят от свойств поверхности. Можно внести в среду, в которой происходит реакция, третий предмет; это также может сильно изменить скорость реакции, такие вещества при незначительном изменении А *иногда чрезвычайно влияют на скорость реакции; их называют катализаторами . Реакции может практически не быть совсем, потому что А *слишком велика для заданной температуры, но если добавить это специальное вещество — катализатор, то реакция протекает очень быстро, потому что А *уменьшается.
Между прочим, эта реакция А плюс В , дающая АВ , доставляет немало волнений. Ведь невозможно сохранить сразу и энергию, и импульс, пытаясь подогнать два предмета друг к другу, чтобы сделать из них один более устойчивый. Следовательно, необходим по крайней мере третий предмет С и реальная реакция выглядит гораздо сложнее. Скорость прямого процесса должна содержать произведение n A n B n C , и можно подумать, что наша формула становится неверной, но это не так! Если мы начнем искать скорость развала АВ , то выясним, что этой молекуле еще надо столкнуться с С , поэтому скорость обратной реакции пропорциональна n AB n C и из формулы для равновесных концентраций n C выпадает. Правильность закона равновесия (42.9), который мы написали прежде всего, абсолютно гарантирована независимо от любого возможного механизма реакции!
Читать дальше


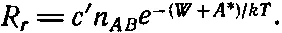 (42.11)
(42.11)




