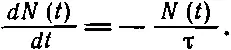 (43.3)
(43.3)
Число молекул, выбывших из игры за промежуток dt , пропорционально числу наличных молекул и обратно пропорционально среднему времени жизни τ. Уравнение (43.3) легко проинтегрировать, если переписать его в виде
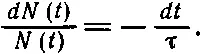 (43.4)
(43.4)
Поскольку в каждой части стоит полный дифференциал, то интеграл уравнения таков:
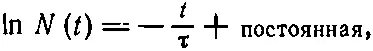 (43.5)
(43.5)
или, что то же самое,
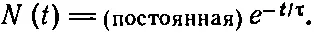 (43.6)
(43.6)
Мы знаем, что постоянная должна быть равна N 0— полному числу молекул, потому что в начальный момент t=0 все молекулы ждут «следующего» удара. Мы можем записать наш результат в виде
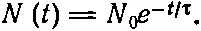 (43.7)
(43.7)
Если мы хотим определить вероятность P ( t ) того, что молекула не испытает столкновений, нужно величину N ( t ) поделить на N 0; тогда получим
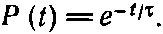 (43.8)
(43.8)
Вот наш результат: вероятность того, что какая-то молекула сможет прожить время t , не столкнувшись, равна ехр(-t/τ), где τ — среднее время между столкновениями. Вероятность эта начинается с 1 (очевидности) при t =0 и уменьшается по мере того, как t становится все больше и больше. Вероятность того, что молекула избежит столкновений за время τ, равна е -1=0,37... Шансов выдержать дольше, чем среднее время между столкновениями, меньше половины. В этом нет ничего странного, потому что существует достаточно много молекул, которые избегают столкновений значительно дольше среднего времени между столкновениями, так что среднее время между столкновениями по-прежнему равно τ.
Первоначально мы определили τ как среднее время между столкновениями. Сформулированный в виде уравнения (43.7) результат говорит нам, что среднее время, отсчитываемое от произвольно взятого момента до следующего столкновения, также равно τ. Этот несколько удивительный факт можно продемонстрировать следующим образом. Число молекул, которые испытают их следующее столкновение в промежутке dt , отсчитанного от времени t после произвольно взятого начального времени, равно N ( t ) dt /τ. Их «промежуток времени до следующего столкновения» равен, конечно, t . «Среднее время до следующего столкновения» получается обычным образом:
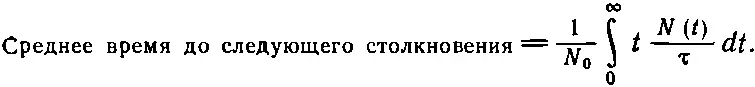
Используя полученное из (43.7) число N ( t ) и вычисляя интеграл, найдем, что τ — это среднее время, отсчитанное от любого момента до следующего столкновения.
§ 2. Средняя длина свободного пробега
Есть еще возможность описать столкновения молекул, не вводя для этого времени между столкновениями. Можно определить, далеко ли успеет уйти частица между столкновениями. Если мы знаем, что среднее время между столкновениями равно τ, а средняя скорость молекул равна v , то очевидно, что среднее расстояние между столкновениями, которое мы обозначим буквой l , равно произведению τ и v. Это расстояние между столкновениями обычно называют длиной свободного пробега :
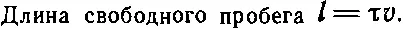 (43.9)
(43.9)
В этой главе мы не будем уточнять, какого рода среднее мы имеем в виду в каждом случае. Существующие разные средние — среднее, корень из среднего квадрата и т. д.— приблизительно равны и отличаются только множителями, близкими к единице. Поскольку для получения правильных множителей необходим подробный анализ, нам нет смысла очень уж стараться уточнять, какое именно среднее используется в том или ином случае. Мы хотим еще предупредить читателей, что используемые для обозначения физических величин алгебраические символы (например, l для длины свободного пробега) не являются общепринятыми просто потому, что об этом никто еще специально не договаривался.
Читать дальше

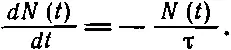 (43.3)
(43.3)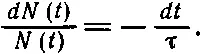 (43.4)
(43.4)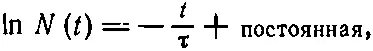 (43.5)
(43.5)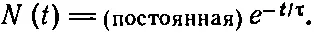 (43.6)
(43.6)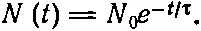 (43.7)
(43.7)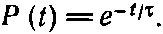 (43.8)
(43.8)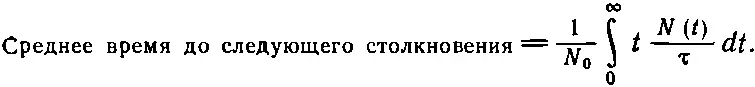
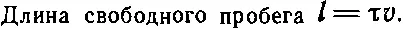 (43.9)
(43.9)




