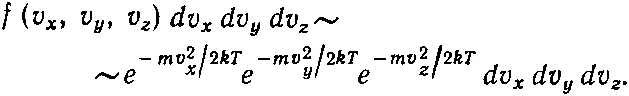 (40.9)
(40.9)
Вы можете убедиться в том, что эта формула верна, ибо, во-первых, распределение зависит только от v 2и, во-вторых, вероятности данных v z получаются после интегрирования по всем v x и v yи это должно привести к (40.7). Но обоим этим требованиям удовлетворяет только функция (40.9).
§ 5. Удельные теплоемкости газов
Посмотрим теперь, как можно проверить теорию и оценить, насколько хороша классическая теория газов. Мы уже говорили, что если U —внутренняя энергия N молекул, то формула pV = NkT =(γ-1) U иногда и для некоторых газов может оказаться правильной. Мы знаем, что для одноатомного газа правая часть равна 2/ 3кинетической энергии движения центров масс атомов. В случае одноатомного газа кинетическая энергия равна внутренней энергии, поэтому γ-1== 2/ 3.
Но предположим, что мы столкнулись с более сложной молекулой, которая может вращаться и колебаться, и предположим (в классической механике это так), что энергии внутренних движений также пропорциональны kT . Поэтому при заданной температуре молекула, кроме кинетической энергии kT , имеет внутреннюю энергию колебания и вращения. Тогда полная энергия U включает не только кинетическую энергию, но и вращательную энергию и мы получаем другие значения у . Наилучший способ измерения γ — это измерение удельной теплоемкости, характеризующей изменение энергии при изменении температуры. К этому способу мы еще вернемся, а пока предположим, что нам удалось экспериментально определить γ с помощью кривой PV γ, соответствующей адиабатическому сжатию.
Попробуем вычислить γ для ряда частных случаев. Прежде всего для одноатомных газов полная энергия U есть не что иное, как кинетическая энергия, и в этом случае, как мы уже знаем, γ равно 5/ 3. В качестве примера двухатомных газов рассмотрим кислород, водород, пары иода и т. д. и предположим, что двухатомный газ можно представить как собрание пар атомов, между которыми действуют силы, похожие на те, что изображены на фиг. 40.3. Можно также предположить, и оказывается, что это вполне законно, что при температурах, обычных для диатомных газов, пары атомов стремятся удалиться друг от друга на расстояние r 0(расстояние минимума потенциальной энергии). Если бы это было не так, и вероятность не очень сильно зависела от удаления от равновесной конфигурации, то мы обнаружили бы, что кислород есть смесь сравнимых количеств O 2и одиночных атомов кислорода. А мы знаем, что в кислороде присутствует очень мало одиночных атомов кислорода, а это означает, что глубина потенциальной ямы значительно больше kT , и это как раз мы и предполагали. Но раз атомы, составляющие молекулу, прочно закреплены на расстоянии r 0, то нам понадобится лишь часть потенциальной кривой вблизи минимума, которую в этом случае можно приближенно заменить параболой. Параболический потенциал соответствует гармоническому осциллятору, и, в самом деле, отличной моделью молекулы кислорода могут служить два соединенных пружинкой атома.
Но чему же равна полная энергия молекулы при температуре Т ? Мы знаем, что кинетическая энергия каждого из атомов равна 3/ 2 kT , так что кинетическая энергия обоих атомов равна 3/ 2 kT + 3/ 2 kT . Можно распределить эту энергию иначе: тогда те же самые 3/ 2плюс 3/ 2будут выглядеть как кинетическая энергия центра масс ( 3/ 2), кинетическая энергия вращения ( 2/ 2) и кинетическая энергия колебаний ( 1/ 2). Известно, что на долю кинетической энергии колебаний приходится 1/ 2, потому что это одномерное движение, а каждой степени свободы соответствует 1/ 2 kT . Обращаясь к вращениям, мы можем выделить две оси вращения, что соответствует двум независимым движениям. Мы представляем себе атомы в виде точек, которые не могут вращаться вокруг соединяющей их линии. Но на всякий случай запомним о таком предположении, потому что если мы упремся где-то в тупик, то, может быть, здесь обнаружится корень зла. Нас должен интересовать еще и другой вопрос: чему равна потенциальная энергия колебаний, велика ли она? Средняя потенциальная энергия гармонического осциллятора равна средней кинетической энергии, т.е. также 1/ 2 kT . Полная энергия молекулы U = 7/ 2 kT , или kT = 2/ 7 U на атом. Это означает, что γ равно 9/ 7, а не 5/ 3, т. е. γ=1,286.
Читать дальше

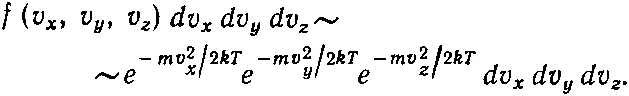 (40.9)
(40.9)




