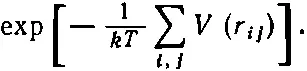Так же, как и раньше, рассечем газ двумя параллельными плоскостями, промежуток между которыми равен dx . Тогда сила, действующая на каждый атом, умноженная на число атомов в 1 см 3(обобщение прежнего nmg ) и умноженная на dx , должна сбалансировать изменение давления: Fndx = dP = kTdn . Или, придав этому закону другую форму, которая пригодится позднее, запишем:
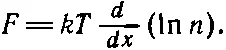 (40.2)
(40.2)
Теперь заметим, что — Fdx — это работа, которую надо совершить для переноса молекулы из х в х + dx , и если сила F произошла из потенциала, т. е. работу можно описывать с помощью потенциальной энергии, то нужную нам величину можно считать изменением потенциальной энергии (п. э.). Отрицательное изменение потенциальной энергии — это произведенная работа Fdx , так что d ( lnn )=- d (п. э.)/ kT , или после интегрирования
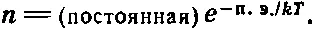 (40.3)
(40.3)
Таким образом, то, что нам удалось заметить в частном случае, справедливо вообще. (А что если F не происходит из потенциала? Тогда (40.2) просто-напросто не имеет решения. В этом случае, после того как какой-нибудь атом опишет замкнутый путь, вдоль которого полная работа не равна нулю, энергия либо прибавится, либо убавится и равновесие никогда не установится. Температурное равновесие невозможно, если внешние силы, действующие на газ, не консервативны.) Уравнение (40.3) известно под названием закона Больцмана . Это еще один из принципов статистической механики: вероятность найти молекулу в заданной точке заданной пространственной конфигурации изменяется экспоненциально, причем показатель экспоненты состоит из потенциальной энергии в заданной пространственной конфигурации, взятой с обратным знаком и деленной на kT .
Таким образом, мы знаем кое-что о распределении молекул. Предположим, что в нашем распоряжении имеется плавающий в жидкости положительный ион; он притягивает окружающие его отрицательные ионы. Много ли их окажется на разных расстояниях от положительного иона? Если нам известно, как зависит от расстояния потенциальная энергия, то отношение чисел ионов на разных расстояниях определяется полученным нами законом. Этому закону можно найти еще много других применений.
В менее элементарной статистической механике пытаются решить следующую важную задачу. Предположим, что имеется совокупность притягивающихся друг к другу молекул и сила между любыми двумя молекулами, скажем i-й и j-й, зависит только от расстояния между ними r ijи может быть представлена в виде производной от потенциальной энергии V(r ij). На фиг. 40.3 показан возможный вид такой функции.
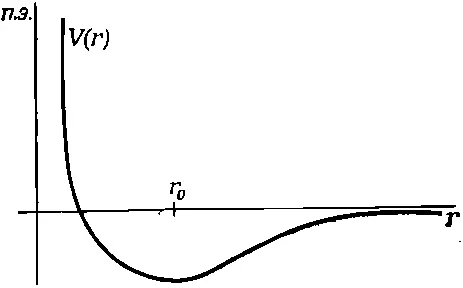
Фиг. 40.3. Кривая потенциальной энергии для двух молекул. Потенциальная энергия зависит только от расстояний.
Если r>r 0, то при сближении молекул энергия уменьшается, поэтому молекулы притягиваются; если же молекулы сближаются еще теснее, энергия очень резко возрастает, значит, на малых расстояниях молекулы сильно отталкиваются. Таково в общих чертах поведение молекул.
Предположим теперь, что мы заполнили этими молекулами какой-то ящик и хотим знать, как они там уместятся в среднем. На это даст ответ выражение ехр(-п. э./kT). В этом случае полная потенциальная энергия, если предположить, что молекулы взаимодействуют только попарно, равна сумме всех парных энергий (в более сложных случаях могут встретиться и тройные силы, но электрические силы, например, парные). Поэтому вероятность того, что молекулы образуют конфигурацию, характеризуемую заданными комбинациями расстояний r ij , пропорциональна
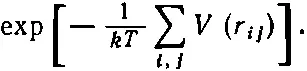
Если температура очень высока, так что kT≫|V(r 0)|, то экспонента почти всюду мала, и вероятность найти молекулу в том или ином месте почти не зависит от расстояния до других молекул. Рассмотрим случай двух молекул; в этом случае ехр (—п.э./kT) будет вероятностью найти молекулы на расстоянии r друг от друга. Ясно, что вероятность максимальна тогда, когда потенциал наиболее отрицателен, а когда потенциал стремится к бесконечности, вероятность почти равна нулю (это происходит на очень малых расстояниях). Это означает, что у атомов газа нет шансов столкнуться друг с другом, уж очень сильно они отталкиваются. Но очень велики шансы найти эти молекулы (если отнести вероятность к единичному объему ) вблизи точки r 0. Здесь вероятность больше, чем в других точках, но насколько больше — это зависит от температуры. Если температура очень велика по сравнению с разностью энергий в точках r= r 0и r=∞, то экспонента всегда почти равна единице. Это случай, когда средняя кинетическая энергия (она порядка kT ) значительно превосходит потенциальную энергию. Силы тогда мало что значат. Но с падением температуры вероятность найти молекулы на расстоянии, близком к r 0, резко возрастает по сравнению с вероятностью найти молекулы в любом другом месте; и в самом деле, если kT много меньше |V(r 0)|, то около r 0экспонента имеет довольно большой положительный показатель. Другими словами, при заданном объеме молекулы предпочитают быть на расстоянии минимальной энергии, а не очень далеко друг от друга. По мере падения температуры атомы сближаются, сбиваются в кучу, объединяются в жидкости, в твердые тела и молекулы, а если их подогреть, то они испаряются.
Читать дальше

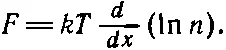 (40.2)
(40.2)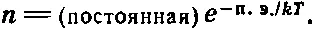 (40.3)
(40.3)