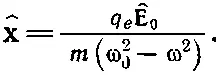 (32.16)
(32.16)
Из этой формулы для ^ xи равенства (32.2) легко получить интенсивность рассеяния в заданном направлении.
Однако, чтобы сэкономить время, вычислим сначала полную интенсивность рассеяния во всех направлениях. Полную энергию, рассеиваемую атомом за 1 сек во всех направлениях, можно получить из формулы (32.7). После перегруппировки членов выражение для энергии принимает вид
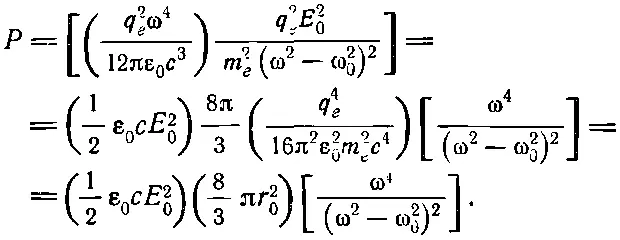 (32.17)
(32.17)
Мы приводим результат в такой форме потому, что она удобна для запоминания: прежде всего, рассеиваемая энергия пропорциональна квадрату падающего поля. Что это означает? Очевидно, квадрат поля пропорционален энергии падающего пучка, проходящей за 1 сек. (В самом деле, энергия, падающая на 1 м 2за 1 сек, равна произведению ε 0с и среднего квадрата электрического поля 2>; если максимальное значение Е есть Е 0то 2>=1/ 2E 0 2.) Другими словами, рассеиваемая энергия пропорциональна плотности падающей энергии; чем сильнее солнечный свет, тем ярче кажется небо.
А какая доля падающего света рассеивается электроном? Вообразим мишень с площадью σ, помещенную на пути луча (не настоящую мишень, сделанную из какого-то вещества, потому что она приведет к дифракции света и т. п., а воображаемую мишень, нарисованную в пространстве). Количество энергии, проходящее через поверхность σ, пропорционально падающей интенсивности и площади мишени:
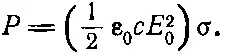 (32.18)
(32.18)
А теперь давайте условимся: полное количество энергии, рассеиваемое атомом, мы приравняем энергии падающего пучка, проходящей через некоторую площадь; указав величину площади, мы тем самым определяем рассеиваемую энергию. В такой форме ответ не зависит от интенсивности падающего пучка; он выражает отношение рассеиваемой энергии к энергии, падающей на 1 м 2. Другими словами,
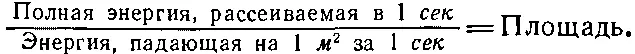
Смысл этой площади заключается в том, что, если бы вся попадающая на нее энергия отбрасывалась в сторону, она рассеивала бы столько энергии, сколько рассеивает атом.
Эта площадь называется эффективным сечением рассеяния. Понятие эффективного сечения используется всегда, когда эффект пропорционален интенсивности падающего пучка. В таких случаях количественный выход эффекта задается площадью эффективной области, выхватывающей из пучка такую часть, чтобы она равнялась выходу. Это ни в коем случае не означает, что наш осциллятор на самом деле занимает подобную площадь. Если бы свободный электрон просто качался взад и вперед, ему бы не соответствовала никакая площадь. Это лишь способ выражения результата через определенную величину; мы указываем площадь, на которую должен упасть пучок, чтобы получилась известная энергия рассеяния. Итак, в нашем случае
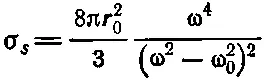 (32.19)
(32.19)
(s — рассеяние).
Рассмотрим несколько примеров. Прежде всего, когда собственная частота очень мала или электрон вообще свободен, что соответствует ω 0=0, частота ω выпадает и сечение σ становится константой. В этом пределе сечение носит название томпсоновского сечения рассеяния. Оно равно площади квадратика со стороной около 10 -15м, т. е. площади 10 -30м 2, а это очень мало!
С другой стороны, при рассеянии света в воздухе собственные частоты осцилляторов, как мы уже говорили, больше частот обычного света. Отсюда следует, что величиной ω 2в знаменателе можно пренебречь и сечение оказывается пропорциональным четвертой степени частоты. Значит, свет с частотой, в два раза большей, рассеивается в шестнадцать раз интенсивнее, а это уже вполне ощутимая разница. Таким образом, голубой свет, частота которого примерно вдвое выше частоты света у красного конца спектра, рассеивается значительно интенсивнее, чем красный свет. И, взглянув на небо, мы видим только изумительную синеву!
Стоит сказать еще несколько слов по поводу полученных результатов. Ответьте, во-первых, почему мы видим облака? Откуда они берутся? Всем известно, что возникают они за счет конденсации водяных паров. Но водяные пары, конечно, находились в атмосфере еще до конденсации. Почему же мы их не видели? А вот после конденсации их прекрасно видно. Не были видны — и вдруг появились. Как видите, тайна происхождения облаков — это совсем не детский вопрос, вроде «Папа, откуда взялась вода?», и ее нужно объяснить.
Читать дальше

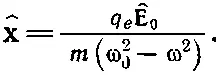 (32.16)
(32.16)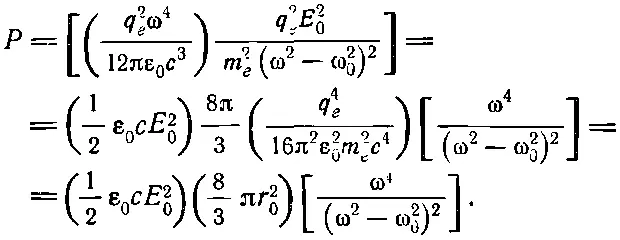 (32.17)
(32.17)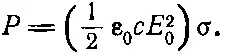 (32.18)
(32.18)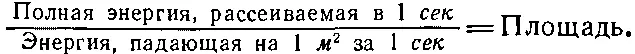
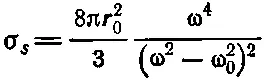 (32.19)
(32.19)




