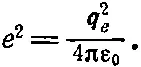 (32.7)
(32.7)
Если это численное значение e подставить в старые формулы, то все остальные величины в них можно считать определенными в системе СИ. Например, формула (32.5) прежде имела вид Р = 2/ 3е 2а 2/с 3. А потенциальная энергия протона и электрона на расстоянии r есть q e 2/4πε 0r или е 2/r, где е =1,5188·10 -14ед. СИ.
§ 3. Радиационное затухание
Заряд, закрепленный на пружине с собственной частотой ω 0(или электрон в атоме), даже в абсолютно пустом пространстве не сможет колебаться бесконечно долго, поскольку, колеблясь, он теряет энергию на излучение. Никаких сил сопротивления в обычном смысле этого слова, никакой вязкости здесь нет. Но колебания не будут происходить «вечно», вследствие излучения они будут медленно замирать. А насколько медленно? Определим для осциллятора величину Q , вызванную так называемым радиационным сопротивлением или радиационным затуханием. Для любой колеблющейся системы величина Q равна энергии системы в данный момент времени, деленной на потери энергии, отнесенные к 1 рад :
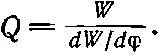
Запишем Q по-другому, пользуясь для этого равенством dW/dφ=(dW/dt)/(dφ /dt)=-(dW/dt)/ω:
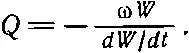
Если Q задано, то легко получить закон спадания энергии колебаний: dW/dt=(-ω/Q)W, откуда следует W=W 0e -ωt/Q; здесь W 0— начальная энергия (при t=0).
Чтобы найти Q для излучающего осциллятора, вернемся к формуле (32.8) и подставим вместо dW/dt выражение (32.6).
А что нужно взять в качестве энергии W осциллятора? Кинетическая энергия осциллятора равна 1/2mv 2, а средняя кинетическая энергия равна mω 2x 0 2/4. Но мы помним, что полная энергия осциллятора равна средней кинетической плюс средняя потенциальная, причем обе они для осциллятора равны; поэтому полная энергия равна
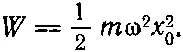 (32.9)
(32.9)
Какую частоту следует подставить в наши формулы? Мы возьмем собственную частоту ω 0, потому что практически это и есть частота излучения атома, а вместо m подставим m e. После ряда сокращений эта формула приводится к виду
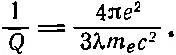 (32.10)
(32.10)
(Для большей ясности и из соображений близости к исторически принятой форме мы ввели величину е 2=q e 2/4πε 0и записали 2π/λ вместо ω 0/с.) Поскольку величина Q безразмерна, множитель е 2/m ес 2, зависящий только от массы и заряда электрона и выражающий его внутренние свойства, обязан иметь размерность длины. Он был назван классическим радиусом электрона, потому что в старых моделях электрона радиационное сопротивление пытались объяснить действием одной части электрона на другие его части, для чего размеры электрона приходилось выбирать порядка e 2/m ec 2. Но эта величина потеряла свой прежний смысл, и никто теперь не считает, что электрон имеет такой радиус. Численное значение классического радиуса электрона следующее:
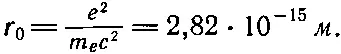 (32.11)
(32.11)
Вычислим теперь значение Q для атома, излучающего видимый свет, например для атома натрия. Длина волны излучения натрия равна примерно 6000 Å и находится в желтой части спектра; эта величина довольно типична. Отсюда
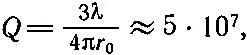 (32.12)
(32.12)
т. е. для атомов Q порядка 10 8. Это значит, что атомный осциллятор колеблется 10 8 рад , или примерно 10 7периодов, прежде чем его энергия уменьшится в 1/ е раз. Частота колебаний света v= с /λ при длине волны 6000 Å составляет 10 15 гц , а, следовательно, время жизни, т. е. время, за которое энергия уменьшится в 1/ е раз, есть величина порядка 10 -8сек.
Примерно за такое же время высвечиваются свободные атомы в обычных условиях. Проведенная оценка справедлива только для атомов в пустом пространстве, не подверженных никаким внешним воздействиям. Если электрон находится в твердом теле, он сталкивается с другими атомами и электронами, и тогда возникает добавочное сопротивление и затухание будет другим.
Читать дальше

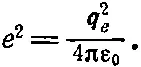 (32.7)
(32.7)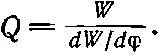
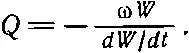
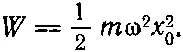 (32.9)
(32.9)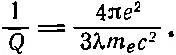 (32.10)
(32.10)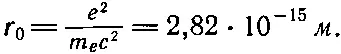 (32.11)
(32.11)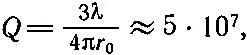 (32.12)
(32.12)




