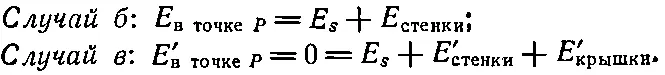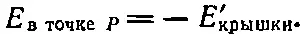Ричард Фейнман - Том 1. Механика, излучение и теплота

Ответим сначала на вопрос: что такое непрозрачный экран? Пусть между источником S и наблюдателем Р находится совершенно непрозрачный экран, как показано на фиг. 31.6, а.

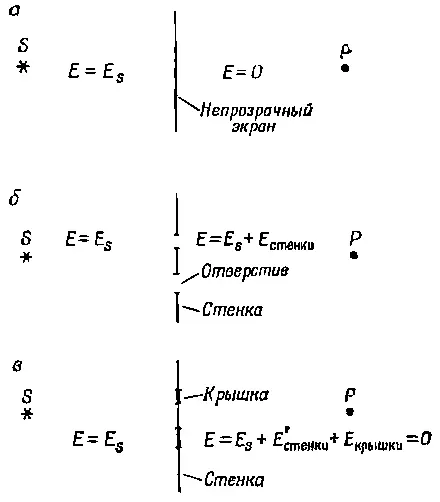
Фиг. 31.6. Дифракция на непрозрачном экране.

Раз экран «непрозрачный», поле в точке Р отсутствует. Почему? Согласно общим принципам, поле в точке Р равно полю E s, взятому с некоторым запаздыванием, плюс поле всех остальных зарядов. Но, как было показано, поле E sприводит заряды экрана в движение, а они в свою очередь создают новое поле, и, если экран непрозрачный, это поле зарядов должно в точности погасить поле E sс задней стенки экрана. Тут вы можете возразить: «Каким чудом они в точности погасятся! А что, если погашение неполное?» Если бы поля гасились не полностью (напомним, что экран имеет некоторую толщину), поле в экране вблизи от задней стенки было бы отлично от нуля. Но тогда оно приводило бы в движение другие электроны экрана, создавая тем самым новое поле, стремящееся скомпенсировать первоначальное поле. Если экран толстый, в нем имеется достаточно много возможностей, чтобы свести остаточное поле к нулю. Пользуясь нашей терминологией, можно сказать, что непрозрачный экран обладает большим и чисто мнимым показателем преломления и поэтому волна в нем экспоненциально затухает. Вам, наверное, известно, что тонкие слои большинства непрозрачных материалов, даже золота, прозрачны.

Посмотрим теперь, какая возникнет картина, если взять такой непрозрачный экран с отверстием, какой изображен на фиг. 31.6, б. Каким будет поле в точке P? Поле в точке Р слагается из двух частей — поля источника S и поля экрана, т. е. поля от движения зарядов в экране. Движение зарядов в экране, по-видимому, очень сложное, но создаваемое ими поле находится довольно просто.

Возьмем тот же самый экран, но закроем отверстия крышками, как показано на фиг. 31.6, в. Пусть крышки сделаны из того же материала, что и экран. Заметьте, что крышки поставлены в тех местах, где на фиг. 31.6, б показаны отверстия. Давайте вычислим теперь поле в точке Р. Поле в точке Р в случае, показанном на фиг. 31.6, в, разумеется, равно нулю, но, с другой стороны, оно также равно полю источника плюс поле электронов экрана и крышек. Мы можем написать следующее равенство:

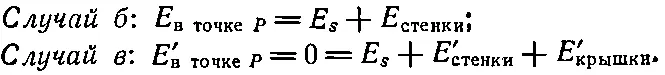
Штрихи относятся к случаю, когда отверстия закрыты крышками; значение E sв обоих случаях, конечно, одно и то же. Вычитая одно равенство из другого, получаем

Если отверстия не слишком малы (например, шириной во много длин волн), то присутствие крышек не должно повлиять на поле у экрана, исключая, быть может, узкую область вблизи краев отверстий. Пренебрегая этим малым эффектом, можно написать E стенки= E ' стенкии, следовательно,

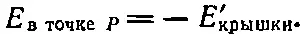
Мы приходим к выводу, что поле в точке Р при открытых отверстиях (случай б) равно (с точностью до знака) полю, создаваемому той частью сплошного экрана, которая находится на месте отверстий! (Знак нас не интересует, поскольку обычно имеют дело с интенсивностью, пропорциональной квадрату поля.) Этот результат не только справедлив (в приближении не очень малых отверстий), но и важен; кроме всего прочего, он подтверждает справедливость обычной теории дифракции.

Поле E ' крышкивычисляется при условии, что движение зарядов всюду в экране создает именно такое поле, которое гасит поле E sна задней поверхности экрана. Определив движение зарядов, мы складываем поля излучения зарядов в крышках и находим поле в точке Р.

Напомним еще раз, что наша теория дифракции приближенная и справедлива в случае не слишком малых отверстий. Если размер отверстий мал, член E ' крышкитакже мал и разность E ' стенки- E стенки(которую мы считали равной нулю) может быть сравнима и даже много больше E ' крышки. Поэтому наше приближение оказывается негодным.