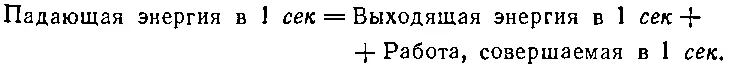 (31.23)
(31.23)
Вместо первого члена можно написать α —Е s 2, где α — коэффициент пропорциональности, связывающий среднее значение —Е 2с энергией, переносимой волной. Во втором члене необходимо включить поле излучения атомов среды, т. е. мы должны записать α —(Е s+E a) 2или (раскладывая квадрат суммы) α( —E s 2+ —2E sE a+ —Е а 2).
Все наши вычисления проводились в предположении, что толщина слоя материала мала и показатель преломления его незначительно отличается от единицы, тогда Е аоказывается много меньше E s(это было сделано с единственной целью — упростить вычисления). В рамках нашего приближения член —Е а 2следует опустить, пренебрегая им по сравнению с —E sE a. Вы можете на это возразить: «Тогда нужно отбросить и —E sE a, потому что этот член много меньше —Е s 2». Действительно, —E sE aмного меньше —Е s 2, но если мы выбросим этот член, то получим приближение, в котором эффекты среды не учитываются совсем! Правильность наших вычислений в рамках сделанного приближения проверяется тем, что мы всюду оставляли члены, пропорциональные N Δ z (плотности атомов в среде), но выбрасывали члены порядка ( N Δ z ) 2и более высоких степеней по N Δ z . Наше приближение можно было бы назвать «приближением малой плотности».
Заметим, кстати, что наше уравнение баланса энергии не содержит энергии отраженной волны. Но так и должно быть, потому что амплитуда отраженной волны пропорциональна N Δ z , а энергия пропорциональна ( N Δ z ) 2.
Чтобы найти последний член в (31.23), нужно вычислить работу, совершаемую падающей волной над электронами за 1 сек. Работа, как известно, равна силе, умноженной на расстояние; отсюда работа в единицу времени (называемая также мощностью) дается произведением силы на скорость. Точнее, она равна F· v, но в нашем случае сила и скорость имеют одинаковое направление, поэтому произведение векторов сводится к обычному (с точностью до знака). Итак, работа, совершаемая в 1 сек над каждым атомом, равна q e —E sv. Поскольку на единичную площадку приходится NΔz атомов, последний член в уравнении (31.23) оказывается равным NΔzq e —E sv. Уравнение баланса энергии принимает вид
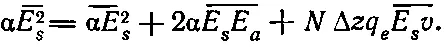 (31.24)
(31.24)
Члены α —E s 2сокращаются, и мы получаем
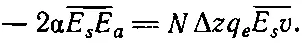 (31.25)
(31.25)
Возвращаясь к уравнению (30.19), находим Е адля больших z:
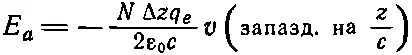 (31.26)
(31.26)
(напомним, что η= N Δ z ). Подставляя (31.26) в левую часть равенства (31.25), получаем
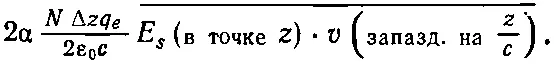
Ho E s(в точке z ) равно E s(в точке атома) с запаздыванием на z / c . Поскольку среднее значение не зависит от времени, оно не изменится, если временной аргумент запаздывает на z / c , т. е. оно равно — E s(в точке атома)·v, но точно такое же среднее значение стоит и в правой части (31.25). Обе части (31.25) будут равны, если выполняется соотношение
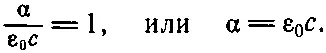 (31.27)
(31.27)
Таким образом, если справедлив закон сохранения энергии, то количество энергии электрической волны, приходящееся на единичную площадку в единицу времени (то, что мы называем интенсивностью), должно быть равно ε 0с —Е 2. Обозначив интенсивность через —S, получим
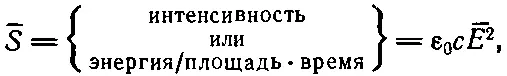 (31.28)
(31.28)
где черта означает среднее по времени. Из нашей теории показателя преломления получился замечательный результат!
§ 6. Дифракция света на непрозрачном экране
Теперь наступил удобный момент, чтобы применить методы настоящей главы к решению задачи другого рода. В гл. 30 мы говорили, что распределение интенсивности света — дифракционную картину, возникающую при прохождении света через отверстия в непрозрачном экране,— можно найти, равномерно распределив источники (осцилляторы) по площади отверстий. Другими словами, дифрагированная волна выглядит так, как будто источником служит дырка в экране. Мы должны выяснить причину этого явления, ведь на самом деле именно в дырке нет источников, нет никаких зарядов, движущихся с ускорением.
Читать дальше

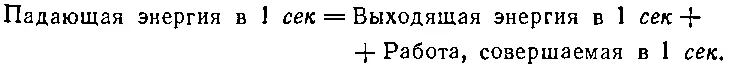 (31.23)
(31.23)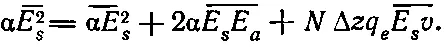 (31.24)
(31.24)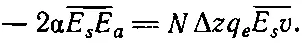 (31.25)
(31.25)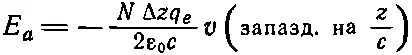 (31.26)
(31.26)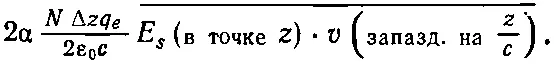
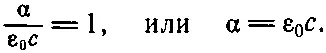 (31.27)
(31.27)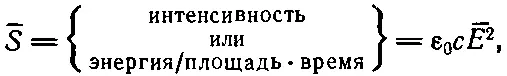 (31.28)
(31.28)




