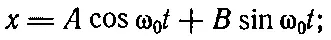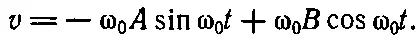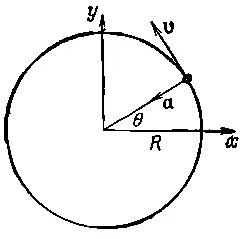
Фиг. 21.2. Частица, движущаяся по кругу с постоянной скоростью.
Тогда d θ/ dt =ω 0= v / R . Известно, что ускорение а=v 2/R=ω 2 0R и направлено к центру. Координаты движущейся точки в заданный момент равны
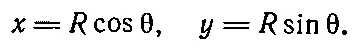
Что можно сказать об ускорении? Чему равна x-составляющая ускорения, d 2 x / dt 2. Н айти эту величину можно чисто геометрически: она равна величине ускорения, умноженной на косинус угла проекции; перед полученным выражением надо поставить знак минус, потому что ускорение направлено к центру:
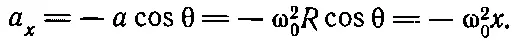 (21.7)
(21.7)
Иными словами, когда частица движется по окружности, горизонтальная составляющая движения имеет ускорение, пропорциональное горизонтальному смещению от центра. Конечно, мы знаем решения для случая движения по окружности: x = Rcos ω 0 t . Уравнение (21.7) не содержит радиуса окружности; оно одинаково при движении по любой окружности при одинаковой ω 0.
Таким образом, имеется несколько причин, по которым следует ожидать, что отклонение грузика на пружинке окажется пропорциональным cosω 0t и движение будет выглядеть так, как если бы мы следили за x-координатой частицы, движущейся по окружности с угловой скоростью ω 0. Проверить это можно, поставив опыт, чтобы показать, что движение грузика вверх-вниз на пружинке в точности соответствует движению точки по окружности. На фиг. 21.3 свет дуговой лампы проектирует на экран тени движущихся рядом воткнутой во вращающийся диск иголки и вертикально колеблющегося груза.
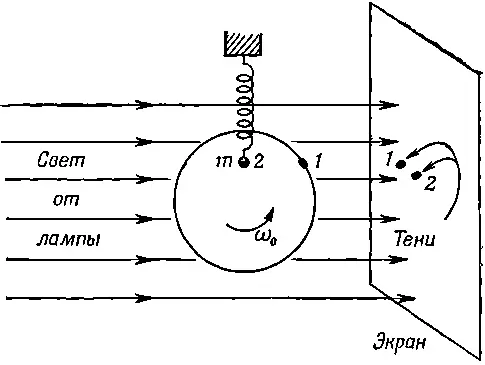
Фиг. 21.3. Демонстрация эквивалентности простого гармонического движения и равномерного движения по окружности.
Если вовремя и с нужного места заставить грузик колебаться, а потом осторожно подобрать скорость движения диска так, чтобы частоты их движений совпали, тени на экране будут точно следовать одна за другой. Вот еще способ убедиться в том, что, находя численное решение, мы почти вплотную подошли к косинусу.
Здесь можно подчеркнуть, что поскольку математика равномерного движения по окружности очень сходна с математикой колебательного движения вверх-вниз, то анализ колебательных движений очень упростится, если представить это движение как проекцию движения по окружности. Иначе говоря, мы можем дополнить уравнение (21.2), казалось бы, совершенно лишним уравнением для у и рассматривать оба уравнения совместно. Проделав это, мы сведем одномерные колебания к движению по окружности , что избавит нас от решения дифференциального уравнения. Можно сделать еще один трюк — ввести комплексные числа, но об этом в следующей главе.
Давайте выясним, какой смысл имеют А и В или а и Δ. Конечно, они показывают, как началось движение. Если движение начнется с малого отклонения, мы получим один тип колебаний; если слегка растянуть пружинку, а потом ударить по грузику — другой. Постоянные А и В или а и Δ, или какие-нибудь две другие постоянные определяются обстоятельствами, при которых началось движение, или, как обычно говорят, начальными условиями . Нужно научиться определять постоянные, исходя из начальных условий. Хотя для этого можно использовать любое из соотношений (21.6), лучше всего иметь дело с (21.6в). Пусть в начальный момент t=0 грузик смещен от положения равновесия на величину х 0и имеет скорость v 0. Это самая общая ситуация, какую только можно придумать. (Нельзя задать начального ускорения , потому что оно зависит от свойств пружины; мы можем распорядиться только величиной х 0.) Вычислим теперь А и В . Начнем с уравнения для
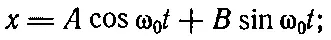
поскольку нам понадобится и скорость, продифференцируем х и получим
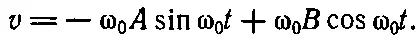
Читать дальше


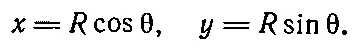
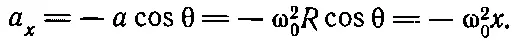 (21.7)
(21.7)