Эти выражения справедливы для всех t , но у нас есть дополнительные сведения о величинах х и v при t=0. Таким образом, если положить t=0, мы должны получить слева х 0и v 0, ибо это то, во что превращаются х и v при t=0. Кроме того, мы знаем, что косинус нуля равен единице, а синус нуля равен нулю. Следовательно,
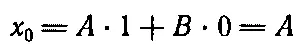
и
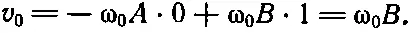
Таким образом, в этом частном случае
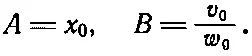
Зная А и В , мы можем, если пожелаем, найти а и Δ.
Итак, задача о движении осциллятора решена, но есть одна интересная вещь, которую надо проверить. Надо выяснить, сохраняется ли энергия. Если нет сил трения, то энергия должна сохраняться. Сейчас нам удобно использовать формулы
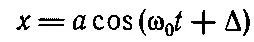
и
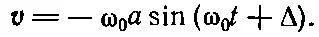
Давайте найдем кинетическую энергию Т и потенциальную энергию U . Потенциальная энергия в произвольный момент времени равна 1/ 2 kx 2, где х — смещение, а k — постоянная упругости пружинки. Подставляя вместо х написанное выше выражение, найдем
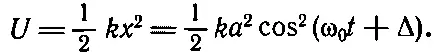
Разумеется, потенциальная энергия зависит от времени; она всегда положительна, это тоже понятно: ведь потенциальная энергия — это энергия пружины, а она изменяется вместе с х . Кинетическая энергия равна 1/ 2 mv 2; используя выражение для v , получаем
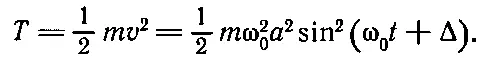
Кинетическая энергия равна нулю при максимальном х, ибо в этом случае грузик останавливается; когда же грузик проходит положение равновесия (x=0), то кинетическая энергия достигает максимума, потому что именно тогда грузик движется быстрее всего. Изменение кинетической энергии, таким образом, противоположно изменению потенциальной энергии. Полная энергия должна быть постоянной. Действительно, если вспомнить, что k = m ω 2 0, то
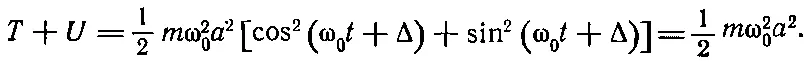
Энергия зависит от квадрата амплитуды: если увеличить амплитуду колебания вдвое, то энергия возрастет вчетверо. Средняя потенциальная энергия равна половине максимальной и, следовательно, половине полной; средняя кинетическая энергия также равна половине полной энергии.
§ 5. Колебания под действием внешней силы
Нам остается рассмотреть колебания гармонического осциллятора под действием внешней силы. Движение в этом случае описывается уравнением
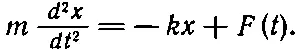 (21.8)
(21.8)
Давайте подумаем, как будет вести себя грузик при этих обстоятельствах. Внешняя движущая сила может зависеть от времени каким угодно образом. Начнем с простейшей зависимости. Предположим, что сила осциллирует
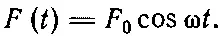 (21.9)
(21.9)
Обратите внимание, что ω — это не обязательно ω 0: будем считать, что можно изменять ω, заставляя силу действовать с разной частотой. Итак, надо решить уравнение (21.8) в случае специально подобранной силы (21.9). Каким будет решение (21.8)? Одно из частных решений (общим решением мы еще займемся) выглядит так:
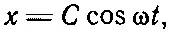 (21.10)
(21.10)
где постоянную С еще надо определить. Иначе говоря, пытаясь найти решение в таком виде, мы предполагаем, что, если тянуть грузик взад и вперед, он в конце концов начнет качаться взад и вперед с частотой действующей силы. Проверим, может ли это быть. Подставив (21.10) в (21.9), получим
Читать дальше

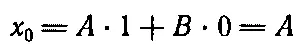
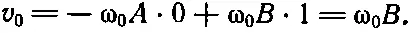
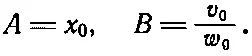
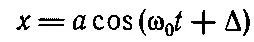
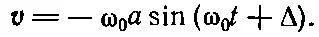
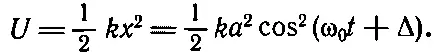
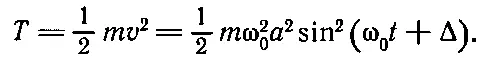
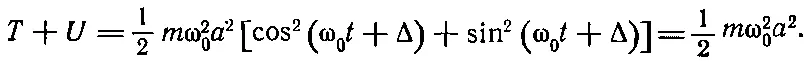
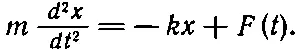 (21.8)
(21.8)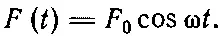 (21.9)
(21.9)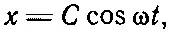 (21.10)
(21.10)




