Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Мы уже знаем, что поначалу струна следует за смычком, пока не срывается с него и не начинает двигаться в обратном направлении. Затем она вновь изменяет направление движения, и ее скорость в конечном итоге вновь сравнивается со скоростью смычка. А возможно ли, чтобы струна не нагнала смычок и трение между ними все время оставалось динамическим? Чего скрипачу стоит опасаться, так это ситуации, о которой говорилось выше на примере опыта с линейкой и веревкой: того, что струна, несмотря на воздействие смычка, вместо того чтобы вибрировать, займет фиксированное положение. В этом случае возвращающая сила натяжения веревки F →будет полностью уравновешивать динамическую силу трения f →(илл. 5b) и струна будет оставаться неподвижной относительно скрипки, а не относительно смычка. Позвольте, но такое положение струны, в котором сумма приложенных к ней сил равна нулю, существует всегда: это положение равновесия.

Так что же, если струна окажется в таком положении, то скрипка замолчит? К счастью, благодаря замечательному свойству канифоли это не так. До тех пор пока смычок покрыт этим веществом (мы по-прежнему предполагаем, что скрипач оказывает постоянное давление на струну), динамическая сила трения f , противореча утверждению закона Амонтона – Кулона, будет уменьшаться с ростом относительной скорости струны относительно смычка (илл. 7).

В рамках очень упрощенного описания (в частности, проигнорировав скручивание струны) мы покажем, что при такой зависимости динамической силы трения от скорости трение приводит не к затуханию колебаний струны, а, наоборот, до определенного предела усиливает их. Равновесное положение струны x 0 в этом случае неустойчиво, и скрипка никогда не замолкнет! Напомним, что равновесие системы может быть как устойчивым, так и неустойчивым. Устойчивое равновесие нам хорошо знакомо: оно соответствует минимуму потенциальной энергии (см. главу 6). Например, шарик на дне полости, слегка отклоненный от равновесия, вернется в исходное положение. Не так обстоит дело с заостренными предметами, например карандашом, когда его прислоняют к стене таким образом, что он стоит, опираясь на кончик. Если при этом его совсем чуть-чуть сместить из положения равновесия, то, в отличие от шара, он упадет влево или вправо и примет другое конечное положение.

Динамическое трение между двумя твердыми телами обычно подчиняется законам, которые в 1699 году установил Гийом Амонтон и в 1781 году уточнил Шарль де Кулон (более известный работами по электростатике). Согласно этим законам, динамическая сила трения не зависит от скорости. Однако она зависит от силы, прилагаемой перпендикулярно к поверхности соприкосновения тел: например, от веса объекта, лежащего на земле, или, в нашем случае, от давления, оказываемого на струну смычком. Отношение же этих сил – так называемый коэффициент трения – от величины приложенной силы не зависит. Оказывается, что он не зависит и от площади контакта между телами, а определяется лишь природой материалов, из которых изготовлены соприкасающиеся тела.

Хотя французские физики Амонтон и Кулон были первыми, кто опубликовал законы трения, по-видимому, двумя веками ранее, судя по его чертежам, с ними был прекрасно знаком и Леонардо да Винчи (1452–1519). Великий тосканский художник был и талантливым физиком.

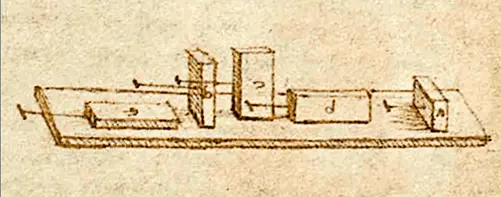
Зарисовка эксперимента Леонардо да Винчи показывает, что коэффициент трения не зависит от площади контактной поверхности (Atlanticus codex, f532r). При постепенном изменении наклона плоскости, на которой лежат тела одинакового веса, изготовленные из одного и того же вещества, однако различающиеся формой, все они начинают скользить одновременно. (По Dowson D. History of Tribology . Longman, New York, 1979)

Ситуация со скрипкой во время фазы скольжения аналогична. Предположим, что струна из положения равновесия x 0 (илл. 5b) отклоняется немного назад, например, из-за неровности смычка. Натяжение струны, пропорциональное ( x – x 0 ), при этом уменьшается, и сила трения, которая направлена противоположно вектору относительной скорости ( v 0 – v ), – тоже! Если сила трения падает быстрее, чем сила натяжения, то отклонение струны назад увеличивается еще больше. Подобная ситуация будет иметь место и при малом отклонении струны от положения равновесия вперед – при этом возрастут и натяжение струны, и сила трения. Если сила трения растет быстрее силы натяжения, то малое отклонение струны вперед от положения равновесия будет развиваться.