Мы пришли в замешательство. Дэниел нас дурачил?
– Я только упростил ситуацию, как и любой физик, – пояснил он. – Применяя теорему Бернулли к жидкости, текущей по трубе, мы предполагаем, что скорость жидкости V относительно стенок одинакова во всей трубе, как в середине, так и по краям. Однако это совсем не так – она постоянно меняется. В частности, скорость жидкости, соприкасающейся со стенками, должна быть равна скорости стенок, то есть нулю! Таким образом, когда поток проходит через трубу небольшого радиуса R и достаточно большой длины L , то скорость жидкости мала по всей толщине трубы. Поток Q в такой трубке определяется по формуле, которую в 1844 году вывел физик Жан Луи Мари Пуазёйль:
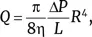
где Δ P – разность давлений между концами трубки и η – коэффициент вязкости жидкости (измеряемый в кг∙м –1∙с –1). Таким образом, при той же разности давлений в одной и той же трубке поток масла окажется меньшим, чем поток менее вязкой воды. И самое главное, из формулы Пуазёйля следует, что при фиксированной разности давлений величина потока очень сильно (по закону R 4) возрастает с увеличением радиуса трубы!
С учетом всех этих эффектов становится понятно, что в случае вытекания жидкости из сосуда через тонкую и не слишком короткую трубу скорость потока оказывается пропорциональной уже не квадратному корню из величины уровня жидкости, а самой этой величине. Кроме того, будучи обратно пропорциональной вязкости жидкости, скорость жидкости начинает зависеть и от природы последней… Именно поэтому выше мы рассматривали достаточно широкую трубу, в которой на некотором отдалении от стенок скорость потока жидкости по поперечному сечению можно считать постоянной. Область же, где скорость существенно изменяется, убывая до нуля при непосредственном контакте со стенкой трубы, – это лишь тонкий пограничный слой .
– И какова толщина этого слоя? – спросила Клаудия.
– Это зависит от величины вязкости жидкости, которая препятствует слишком быстрому изменению скорости по мере удаления от стенок. Так, для масла пограничный слой толще, чем для воды. Более точно, материальные параметры, определяющие толщину вязкого слоя для конкретной жидкости, входят в комбинации η/ρ, где ρ – плотность жидкости. Последняя составляет около 10 –6м 2/с для воды и 1,4∙10 –5м 2/с для воздуха при нормальных условиях.
Дэниел достал записную книжку и карандаш, чтобы выполнить некоторые расчеты.
– Известно, что для трубы длины L , в которой поток жидкости движется со скоростью V , толщина l пограничного слоя оказывается порядка 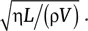 Таким образом, для 250-метрового поезда, движущегося со скоростью 180 км/ч, толщина l составляет несколько сантиметров. Это расстояние достаточно мало по сравнению с расстоянием между поездом и стенкой туннеля, поэтому им можно пренебречь, и теорема Бернулли в рассмотренном выше случае действительно применима. Аналогично для потока воды скоростью 1 м/с в трубе длиной 1 м l оказывается порядка миллиметра…
Таким образом, для 250-метрового поезда, движущегося со скоростью 180 км/ч, толщина l составляет несколько сантиметров. Это расстояние достаточно мало по сравнению с расстоянием между поездом и стенкой туннеля, поэтому им можно пренебречь, и теорема Бернулли в рассмотренном выше случае действительно применима. Аналогично для потока воды скоростью 1 м/с в трубе длиной 1 м l оказывается порядка миллиметра…

6. Резкое открытие крана или клапана может спровоцировать опасное избыточное давление в трубопроводе – гидравлический удар. Этим термином пользуются также и для обозначения возникающих в трубе при закрытии крана после резкого выключения воды неразрушающих ее колебаний. Они сопровождаются характерным глухим шумом
Еще один нюанс: гидравлический удар
Слово взял Пол.
– Кажется, я понял, почему все эти потоки в трубах в начале нашего разговора повысили мое давление! Как-то раз я уехал из дома на всю зиму. Перед отъездом я слил воду из труб и перекрыл краны. Весной, по возвращении, я, не открыв заранее краны, резко пустил воду в домашний трубопровод, и все его сварные швы лопнули. Я позвонил водопроводчику, и он объяснил, что произошел гидравлический удар (илл. 6).
– Возможно, – сказал Дэниел. – Городской водораспределитель и так подает воду в дом под давлением, заметно превышающим атмосферное. При резком же открытии клапана вода может приобрести столь высокую скорость, что инерция позволит ей сжать воздух в трубе вплоть до давления, разрушающего трубу.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

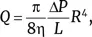
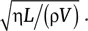 Таким образом, для 250-метрового поезда, движущегося со скоростью 180 км/ч, толщина l составляет несколько сантиметров. Это расстояние достаточно мало по сравнению с расстоянием между поездом и стенкой туннеля, поэтому им можно пренебречь, и теорема Бернулли в рассмотренном выше случае действительно применима. Аналогично для потока воды скоростью 1 м/с в трубе длиной 1 м l оказывается порядка миллиметра…
Таким образом, для 250-метрового поезда, движущегося со скоростью 180 км/ч, толщина l составляет несколько сантиметров. Это расстояние достаточно мало по сравнению с расстоянием между поездом и стенкой туннеля, поэтому им можно пренебречь, и теорема Бернулли в рассмотренном выше случае действительно применима. Аналогично для потока воды скоростью 1 м/с в трубе длиной 1 м l оказывается порядка миллиметра…



![Лина Сайфер - Театр мыльных пузырей [litres]](/books/434478/lina-sajfer-teatr-mylnyh-puzyrej-litres-thumb.webp)






