– Конечно, – согласился Дэниел. – Впрочем, это обстоятельство учитывалось в экспериментальном устройстве, с помощью которого Бернулли доказывал свою формулу. Жидкость текла по вертикальной трубе, установленной в нижней части сосуда (илл. 5). В этом случае поток оказывался не горизонтальным, как в туннеле, и теорему Бернулли необходимо было формулировать в более общей форме. А именно, в любой точке жидкости:
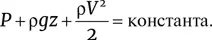
g – ускорение свободного падения и z – высота, P и V – по-прежнему давление и скорость потока (на высоте z ), а ρ – плотность жидкости. Исторически Бернулли уделял особое внимание конкретной проблеме: продолжительности вытекания жидкости из сосуда через малое отверстие (см. главу 10, врезку «Вытекание жидкости из сосуда и советы водопроводчика»).
Вязкость и пограничный слой
– Вопрос вытекания жидкости из сосуда через отверстие уже изучался за столетие до Бернулли, в частности итальянским ученым Эванджелистой Торричелли. Последний заметил, что скорость потока не зависит от характера жидкости и формы сосуда и оказывается пропорциональной квадратному корню из h – высоты жидкости в сосуде. Однако этот результат был приблизительным, как и многие вещи, о которых я только что рассказал…
Вытекание жидкости из сосуда и советы водопроводчика
Изучая конкретный случай вытекания воды из какого-либо сосуда, мы увидим, что теорему Бернулли следует применять с определенной осмотрительностью.
Читатель легко может поставить следующий опыт, схема которого приведена ниже. Нальем воду в пластиковую бутылку с продырявленным дном и станем измерять время τ, за которое она опустошается, в зависимости от уровня ее начального наполнения H . Как связаны эти величины?
На первый взгляд можно решить, что величина P + ρ gh + ρ V 2/2 (здесь h – высота уровня воды в емкости в данный момент) одинакова на поверхности жидкости и на выходе ее из отверстия. При этом и давление на обоих уровнях должно быть равно атмосферному давлению P 0 . Предполагая, для простоты, что площадь сечения S емкости намного больше площади отверстия s , можно легко определить скорость потока V в момент, когда высота столба воды в нем есть h :
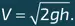
Заметим, что эта скорость равна скорости, которой достигает изначально неподвижное тело, упавшее с высоты h .
На самом же деле полученный ответ дает нам лишь порядок искомой величины, поскольку использование выше формулы Бернулли было основано на предположениях, которые не совсем точны. Давление на выходе из отверстия действительно равно P 0 , но только на поверхности струи, а не внутри. У дна сосуда давление оказывается бóльшим: оно равно давлению на поверхности, к которому добавляется вес столба жидкости, то есть P 0 + ρ gh . Оно не может резко, скачком, уравняться с давлением P 0 по всему объему рассматриваемого элемента струи, это выравнивание происходит постепенно. Таким образом, на выходе из отверстия скорость внутри струи оказывается меньшей, чем скорость воды у поверхности струи V . В конечном итоге скорость потока оказывается меньшей, чем следовало ожидать из приведенной выше оценки. Приведенная выше величина V умножается на коэффициент C , меньше или равный 1, величина которого зависит от геометрической формы отверстия: для кругового отверстия, просверленного непосредственно в нижней части сосуда, он близок к 0,6. Время слива τ с учетом этого коэффициента определяется так:
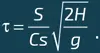
Коэффициент C может быть изменен путем оснащения отверстия приспособлением под названием «штуцер» (на илл. представлен в виде красной трубы). Штуцеры являются частью арсенала водопроводчиков: добавляя короткую трубу к отверстию потока, они таким образом могут влиять на форму и мощность струи.
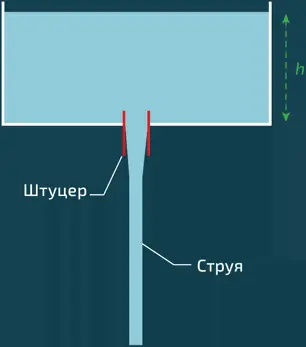
Вытекание жидкости из сосуда, заполненного до высоты h . Теорема Бернулли подразумевает, что скорость слива пропорциональна 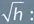 таким образом, она уменьшается по мере того, как емкость пустеет
таким образом, она уменьшается по мере того, как емкость пустеет
Читать дальше
Конец ознакомительного отрывка
Купить книгу

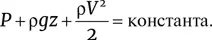
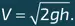
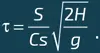

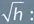 таким образом, она уменьшается по мере того, как емкость пустеет
таким образом, она уменьшается по мере того, как емкость пустеет


![Лина Сайфер - Театр мыльных пузырей [litres]](/books/434478/lina-sajfer-teatr-mylnyh-puzyrej-litres-thumb.webp)






