Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Так что, разве точное установление «числа поцелуев» в пространстве не дало ответ на задачу Кеплера? Увы, нет! Существует множество способов размещения 12 периферийных шаров вокруг центрального, что делает задачу очень сложной. Один из таких способов упаковки – это гранецентрированная кубическая решетка (см. главн 8, «Задача с многочисленными решениями»). Центры соседних шаров в этом случае образуют неправильный многогранник, называемый кубоктаэдром Кеплера (ниже). Он имеет 14 граней (восемь равносторонних треугольников и шесть квадратов). На треугольных гранях кубоктаэдра три шара уложены максимально компактно, так как ребра этих граней равны диаметру шаров и, следовательно, шары никак не могут располагаться ближе друг к другу. То же самое можно сказать и о квадратных гранях.

Когда вокруг центрального шара располагают 12 периферийных без какого-то особого порядка, то их центры обычно образуют икосаэдр (многогранник с 20 треугольными гранями), который может быть как правильным, так и неправильным. Если вычислить длину ребер икосаэдра, окажется, что они больше диаметра шаров [8] Далее приведены основные этапы расчета для регулярного икосаэдра. Объем кубоктаэдра где а – диаметр шариков. Объем икосаэдра: где b – длина ребра. Квадрат соотношения b/a равен 8sin 2 (π/5)/[3 + sin 2 (π/5) – cos(π/5)], углы выражаются в радианах. Таким образом, b/a = 1,044. . Таким образом, можно немного изменять положение периферийных шаров, не отрывая их от центрального шара.

Даже когда очевидно, что наиболее компактная укладка шаров – укладка такими многогранниками, еще предстоит определить, какими именно. Кубоктаэдром? Икосаэдром? Обычный икосаэдр имеет меньший объем, но пространство невозможно заполнить путем укладки правильных икосаэдров. Вот насколько сложна задача Кеплера…

Сколько одинаковых монет можно разложить на столе, чтобы они касались монетки, помещенной в центре? Легко продемонстрировать, что можно разместить максимум шесть штук

В пространстве размещается максимум 12 одинаковых шаров (зеленого цвета на илл.) вокруг центрального шара (синего цвета). Однако между зелеными шарами остается свободное пространство, это позволяет предположить, что возможно вместить и 13-й шар

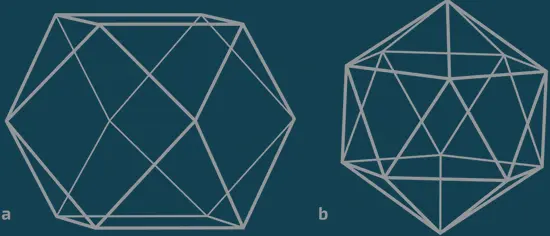
a. Фигура, образованная окружением атома в гранецентрированном кубическом кристалле, представляет собой кубоктаэдр Кеплера. (Примечание: мы перевернули этот многогранник, поэтому вертикальная ось на илл. а не совпадает с вертикальной осью на илл. 7b.) b.Еще один 12-вершинный многогранник: обычный икосаэдр

Удивительно, но описанная нами укладка не уникальна. Есть два способа уложить второй слой шаров на первый, но они эквивалентны. Но вот третий слой может быть размещен двумя различными способами. Так, его можно расположить строго над первым слоем (илл. 7a) или же сместить относительно него (илл. 7b). При укладке каждого последующего слоя возможны оба варианта, поэтому задача Кеплера имеет бесконечное количество решений. Эта множественность решений и влечет за собой всю сложность задачи (см. врезку). Среди всех этих решений два имеют особое значение:

а) упаковка, получаемая путем размещения n -го слоя строго над ( n – 2)-м слоем независимо от n ;

b) упаковка, получаемая путем смещения n -го слоя относительно ( n – 2)-го слоя.

Природа дает нам многочисленные примеры структур, которые следуют одному из этих правил, например некоторые кристаллы. Кристаллы сформированы из периодически повторяющихся «упаковок» атомов, молекул или ионов в пространстве (см. также главу 9, «Случайно расположенные шарики»). Построенные по правилу (a) кристаллические структуры называют «плотноупакованными гексагональными»; по правилу (b) – «гранецентрированными кубическими структурами». Многие химические элементы, например кобальт, цирконий, имеют гексагональную плотноупакованную структуру.

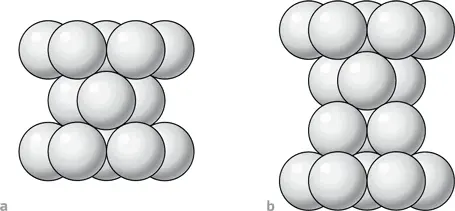
7. Компактная упаковка шаров. a.Случай, когда третий слой помещается строго над первым (гексагональная упаковка). b.Случай, когда третий слой смещен относительно первого. В таком случае четвертый слой находится над первым (кубическая гранецентрированная решетка)