А теперь давайте выйдем из плоскости. Шары реального мира трехмерны, как и само пространство. Как можно их разместить наиболее компактным способом? Давайте попробуем: разумно будет для начала сформировать компактный плоский слой в соответствии с илл. 2. Затем выложим сверху идентичный слой, убедившись, что число точек соприкосновения максимально. Если это так, то каждый шар верхнего слоя касается трех шаров нижнего слоя, и наоборот (илл. 5a). Затем кладем третий слой, чтобы каждый из его шаров коснулся трех шаров второго слоя, и т. д. В результате каждый шар касается еще 12 шаров: шести в том же слое, трех в нижнем и трех в верхнем (илл. 5b). То же самое происходит и в следующих слоях.

4. Покрытие плоскости треугольниками. Центры дисков с илл. 2а образуют такую «сеть из треугольников»
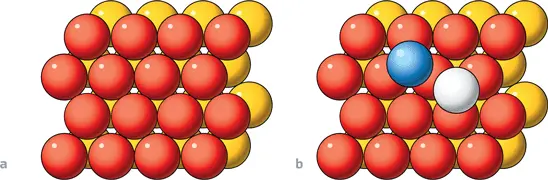
5. Пример наиболее компактной упаковки шаров. a.На компактный плоский слой (желтого цвета) укладывается идентичный слой (красного цвета) таким образом, чтобы каждый красный шар касался трех желтых шаров. b.Третий слой может быть уложен двумя различными способами, при этом шары в нем либо расположены строго над шарами первого слоя (как синий шар), либо смещены (как белый шар)
Решили ли мы задачу? Является ли такая упаковка шаров наиболее плотной? Да, считал ученый XVII века Иоганн Кеплер (более известный открытием траектории движения планет вокруг Солнца. Он доказал, что планета описывает вокруг Солнца эллипс, в одном из фокусов которого оно и находится). Но у Кеплера не было доказательства для задачи об укладке шаров. В отличие от двумерного случая, строгое доказательство действительно очень сложно! Так сложно, что задача об укладке шаров (часто называемая «задачей Кеплера») фигурирует в известном списке, составленном в начале XX века немецким математиком Давидом Гильбертом, где были собраны приоритетные, на его взгляд, математические задачи.
Только в 1998 году американский математик Томас Гейлс объявил, что он решил эту задачу (см. врезку). Как и ожидалось, Кеплер был прав: упаковка компактных двумерных слоев действительно оказывается наиболее компактной трехмерной реализацией (илл. 6). Процент пространства, заполненного шарами, в таком случае составляет около 74 %. Если быть более точными, то читатель, имеющий достаточно храбрости [7] Приведем основные этапы расчета: в каждом слое N 1 центров N 1 шаров радиусом R образуется сеть из N 1 ромбов площадью (отсюда рассчитывается и доля площади плоскости, покрытой дисками: Расстояние между двумя слоями – Если имеется N шаров, то они занимают общий объем тогда как полный объем самих шаров составляет 4π NR 3 /3.
, может убедиться, что доля объема пространства, заполненного шарами, составляет 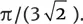 Это довольно мало.
Это довольно мало.

6. Витрина с апельсинами – практический пример компактной укладки твердых шаров
«Поцелуи» шаров в задаче Кеплера
В описанных выше компактных укладках каждый шар контактирует с 12 соседями. Но если рассматривать только один центральный шар, то, возможно, удастся расположить вокруг него большее количество шаров? И сколько шаров в таком случае можно разместить в общей сложности вокруг одного? Это максимальное число в английском языке называют kissing number («число поцелуев» между шарами).
Аналогичная задача в двумерном пространстве уже обсуждалась в разделе «Если бы мир был плоским…». На основе рассуждений или из опыта (ниже) легко увидеть, что «число поцелуев» на плоскости равно шести. Если еще несколько раз воспроизвести полученную локальную упаковку, то так можно замостить всю плоскость.
Для трехмерного случая решение не столь очевидно. Чтобы получить представление о явлении, ничто не помогает так, как наглядный эксперимент! Если у вас найдется достаточное количество мячиков или шаров для пинг-понга, скрепите их суперклеем; или, еще проще, чтобы не испачкаться, положите шарики в прозрачный пакет и попытайтесь сделать его как можно компактнее. Вы убедитесь, что более 12 шаров разместить вокруг центрального не удается. Тем не менее место между ними еще остается, и можно предположить, что, как-то постаравшись, 13-й шар можно было бы между ними вписать (см. илл. далее). В XVII веке этот вопрос стал предметом полемики между Исааком Ньютоном и математиком Дэвидом Грегори. Последний, в отличие от Ньютона, как раз и считал, что рядом с центральным шаром возможно втиснуть и 13-й шар. Сегодня мы знаем, что прав был Ньютон; доказательство этого впервые было найдено лишь через три столетия, в 1953 году.
Читать дальше
Конец ознакомительного отрывка
Купить книгу



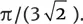 Это довольно мало.
Это довольно мало.



![Лина Сайфер - Театр мыльных пузырей [litres]](/books/434478/lina-sajfer-teatr-mylnyh-puzyrej-litres-thumb.webp)






