Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Интуиция подсказывает, что именно такая упаковка, как на илл. 2а, наиболее компактная из всех возможных. Каждый диск касается еще шести, и невозможно сделать так, чтобы он касался большего количества дисков. Тем не менее тот факт, что количество точек соприкосновения между дисками является максимальным, еще не является достаточным доказательством того, что пространство, занимаемое заданным числом дисков, минимально. Точное доказательство было найдено лишь в XX веке.

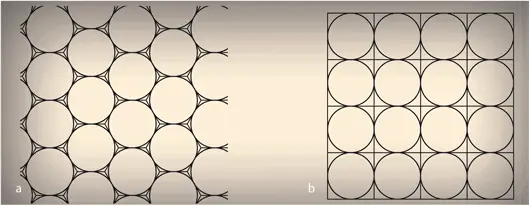
2. Два типа упаковки одинаковых дисков на плоскости. a.Наиболее компактная упаковка. b.Менее компактная упаковка, при которой диски вписываются в квадратную сетку

Можно заметить, что диски при наиболее компактной упаковке могут быть вписаны в шестиугольники, которые полностью покрывают плоскость, – как, например, терракотовая плитка (илл. 2а): в таком случае говорят, что происходит «замощение» плоскости шестиугольниками. Именно такое мощение шестиугольниками осуществляют пчелы для постройки сот (илл. 3). Есть лишь два других способа замостить плоскость одинаковыми правильными многоугольниками: квадратами (илл. 2b) или треугольниками (илл. 4).

3. Создавая соты, пчелы выстраивают их шестиугольниками. Возможно, такое расположение максимально удобно для личинок. К тому же оно экономит воск. В самом деле, длина границ, разделяющих области равных площадей, будет наиболее короткой при упаковке правильными шестиугольниками

Это утверждение легко доказывается. В правильном многоугольнике, у которого n сторон, каждый угол равен α = 180° – 360°/ n . С другой стороны, если каждая вершина многоугольника является общей с ( m – 1) другими многоугольниками, то α = 360°/ m . Поэтому для целых чисел m и n должно выполняться условие 2/ m = 1 – 2/ n , что возможно лишь для n = 3, 4 или 6 (в чем читатель может убедиться без особых усилий). В частности, невозможно выложить паркет из правильных пятиугольников!

Хотя для задачи компактной укладки дисков почти нет практического применения, в реальном трехмерном мире часто рассматривается аналогичная задача (просто заменим диски на цилиндры). Например, электрические провода (цилиндрической формы) обычно собираются в компактные пучки. Это относится и к сверхпроводящим кабелям (см. главу 25, «Технология сверхпроводящих кабелей»), которые состоят из множества сверхпроводящих жил, заключенных в медную оболочку. Изначально провода имеют цилиндрическую форму, но после обжатия они превращаются в шестиугольные призмы!

В отличие от «классических» математических доказательств, написанных на языке формул, доказательство гипотезы Кеплера американский математик Томас Гейлс частично доверил компьютеру. Использование программных продуктов, помогающих ученым в их работе, бурно развивается в последние десятилетия. Подобное программное обеспечение помогает математикам в поисках решений как давно существующих, так и новых открытых проблем. К тому же они освобождаются и от скрупулезной проверки, которую теперь выполняет компьютер, – ведь его вычислительная мощность намного выше человеческой.

Полное доказательство, предложенное Гейлсом, представляет собой серию статей на более чем 250 страницах, а компьютерные коды занимают почти три гигабита памяти. Кто бы взялся прочесть их во всех подробностях и полностью вникнуть в суть доказательства Гейлса? Даже используя помощь компьютера, рецензенты статьи, опубликованной Гейлсом в 2005 году в Annals of Mathematics [6] Математический журнал, основанный в 1874 году и ныне издаваемый раз в два месяца Принстонским университетом и Институтом перспективных исследований. – Прим. пер. , не взялись утверждать, что предложенное им доказательство гипотезы Кеплера безупречно. И только в августе 2014 года команда Гейлса представила аргументы, которые привели к окончательному официальному признанию его доказательства! Как бы там ни было, но все и так давно были уверены, что предложенная Кеплером упаковка является максимально компактной. Ведь если бы это было не так, то за более чем три столетия кто-нибудь нашел бы лучшую, не так ли?