Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

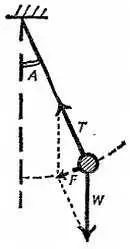
Фиг. 259. К задаче 5.

Задача 6

Это соотношение между силой и отклонением от положения равновесия должно выполняться на любой стадии колебания. Это выглядит похожим на ___

Задача 7

Исходя из задачи 6 , мы можем ожидать, что движение, при котором период Т не зависит от амплитуды, будет наблюдаться для таких тел, как ___, причем для этих тел независимость периода от амплитуды, по всей вероятности, должна быть

_______________________

(ограничена малой амплитудой? не ограничена? или?)

Простое гармоническое движение

Все изохронные колебания представляют собой движения одного и того же типа с одинаковым по форме графиком зависимости амплитуды от времени — синусоидой . Мы называем такое движение простым гармоническим движением (эпитетом «гармоническое». Это движение обязано тому важному значению, которое оно имеет в музыке). Колебания маятника при малых отклонениях очень близки к простым гармоническим движениям. Груз, подвешенный на пружине, движется вверх и вниз, совершая при этом простые гармонические движения в широких пределах изменения амплитуды. (Проделайте наскоро опыт в лаборатории: он доставит вам большое удовлетворение.) Пружина с подвешенным грузом, гибкий брус, растягиваемая проволока, закручиваемый стержень, любая упругая система, подчиняющаяся закону Гука , совершает колебательное движение, называемое простым гармоническим колебанием .

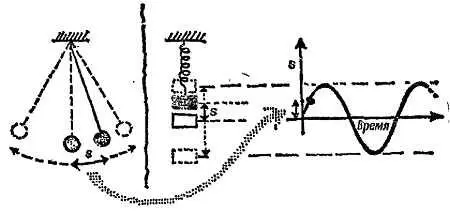
Фиг. 260. Изохронные колебания и график зависимости смещения от времени.

«Простым гармоническим движением» мы называем повторяющееся движение особого типа — движение маятника и схожее с ним движение груза на пружине, — это не просто любое движение с постоянным периодом. (Кроты, выползающие из-под земли каждое утро в поисках пищи и возвращающиеся каждую ночь обратно под землю, совершают в известном смысле «изохронное» движение — его период составляет 24 часа, как бы ни были глубоки их норы, — но это, разумеется, отнюдь не простое гармоническое движение.) Если проанализировать движение маятника, обратившись к геометрии, то можно установить важную характеристику этого движения.

Движение маятника характеризуется переменным ускорением , которое всегда направлено к среднему положению и изменяется прямо пропорционально расстоянию от этого положения.

Если s — расстояние вдоль траектории, скажем, груза маятника, а а — ускорение, то мы найдем a ~ s , или а= —k 2 s, где k — вещественная постоянная.

Знак минус показывает, что ускорение направлено в сторону, противоположную отклонению. (Когда груз отклонен вправо — мы считаем такие отклонения положительными, когда ускорение направлено влево, мы приписываем ему отрицательное значение.)

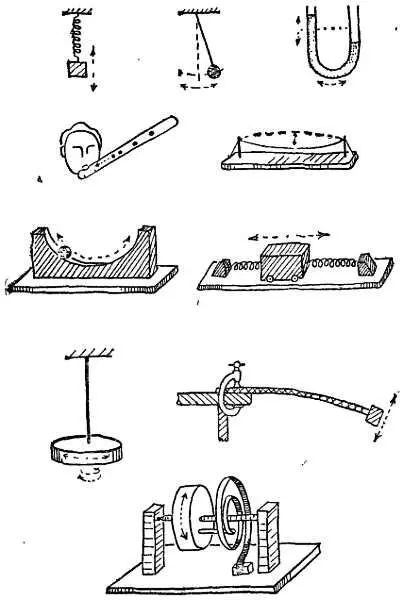
Фиг. 261. Разнообразные системы, совершающие простые гармонические движения.

Механика движения маятника

Чтобы показать, что для груза маятника а ~ s (при малых амплитудах), рассмотрим действующие на него силы. Сила натяжения нити направлена по радиусу и не может изменить скорость груза. Кроме этой силы, на груз действует только притяжение Земли, вес груза, направленный вертикально вниз. Разложим этот вектор на компоненты F 1и F 2:

F 1 направленная вдоль дуги, придает грузу ускорение,

F 2направленная вдоль радиуса, уравновешивает натяжение нити.

Из рассмотрения подобных треугольников (фиг. 262) находим

СИЛА F 1ПРИДАЮЩАЯ УСКОРЕНИЕ / ВЕС Mg= РАССТОЯНИЕ ПО ГОРИЗОНТАЛИ х/ ДЛИНА L

F 1/ Mg = x/ L

Следовательно,

F 1 = Mg∙ x/ L

и

УСКОРЕНИЕ ГРУЗА = СИЛА/МАССА = — F 1/ M= (- Mg∙ x/ L)/ M= — g∙ x/ L

Таким образом, мы установили, что а направлено к положению равновесия и что а ~ х , но мы не получили соотношения a ~ s вдоль траектории движения маятника. При больших отклонениях маятника его движение не является простым гармоническим движением. При малых отклонениях оно почти в точности совпадает с простым гармоническим движением, и х (горизонтальное смещение груза) почти совпадает с криволинейной дугой s (отклонением груза, измеренным вдоль его траектории).