Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

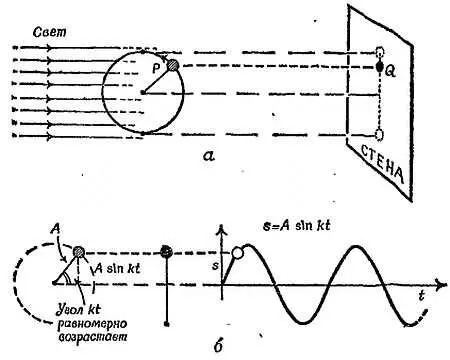
Фиг. 266. Проекция движения по окружности.

Тогда точка Q (тень точки Р ) будет двигаться вверх и вниз. Можно показать, что график зависимости смещения точки Q от времени представляет собой синусоиду (с уравнением s= A∙sin k t , где А — радиус окружности), а это, как мы знаем, и есть временная зависимость простого гармонического движения. Поэтому проекция движения по окружности представляет собой простое гармоническое движение.

На фиг. 267 и 268 схематически показаны опыты, позволяющие сравнить движение маятника или колеблющейся пружины с проекцией движения по окружности. (Инженерам-электрикам часто приходится иметь дело с переменным током, который представляет собой простые гармонические колебания и графически изображается синусоидой. Чтобы производить свои расчеты в сжатой форме, инженеры представляют такие токи или напряжения вращающимся радиусом-вектором, равным амплитуде тока или напряжения; конец этого радиуса-вектора описывает окружность. При вычислениях оперируют проекциями радиуса-вектора. Это считают само собой разумеющимся и обычно упускают из виду.)

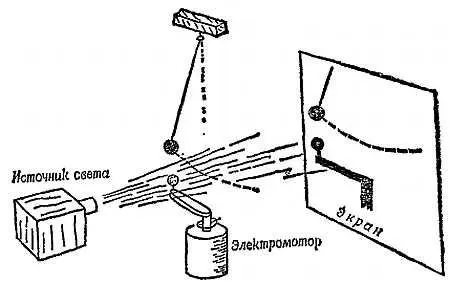
Фиг. 267. Груз маятника движется в такт с проекцией точки, движущейся по кругу.

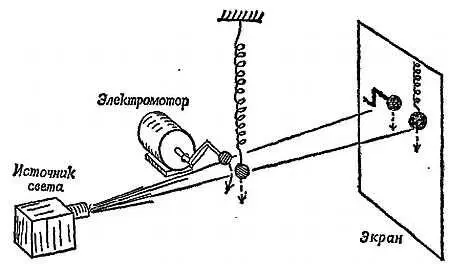
Фиг. 268. Груз, подвешенный на пружине, движется в такт с проекцией точки, движущейся по кругу.

На вал электрического двигателя (например, небольшого двигателя для электрических часов) насажен рычаг, изогнутый под прямым углом, к концу которого прикреплен шар В ; при вращении двигателя шар описывает окружность. Движение тени, отбрасываемой на стенку шаром S , сравнивается с движением тени от груза небольшого маятника. Если правильно выбрать длину маятника и начальную стадию его колебания, то обе тени будут двигаться строго в такт. Подобным же образом можно добиться того, чтобы движения тени шара В и груза, подвешенного на пружине, все время оставались согласованными.

Различные определения простого гармонического движения

Существует несколько определений простого гармонического движения:

4. Это движение взад и вперед , совершаемое грузом маятника (при малых отклонениях), или движение вверх и вниз , которое совершает груз, подвешенный на пружине (или любая другая система, подчиняющаяся закону Гука).

2. Это возвратно-поступательное движение, при котором ускорение (направленное вдоль траектории движения всегда к центру отрезка перемещения) изменяется прямо пропорционально смещению от центра .

3. Это проекция кругового движения , совершаемого с постоянной скоростью (например, круговое движение, каким оно представляется при наблюдении в плоскости круга, или движение тени, которую отбрасывает на землю тело, движущееся по окружности, лежащей в вертикальной плоскости, при освещении вертикальным солнечным светом).

4. Это движение, в случае которого график зависимости смещения от времени представляет собой синусоиду .

Математика, а также простые соображения из механики в первом определении показывают, что во всех случаях происходит одно и то же движение. Чтобы связать воедино приведенные определения, здесь требуется лишь проделать некоторые выкладки и указать на ряд опытов.

Значение простого гармонического движения

Простое гармоническое движение играет такую же важную роль в описании природы, как движения с постоянной скоростью и с постоянным ускорением, поскольку:

1. Этот вид движения весьма распространен (примерами могут служить маятники, музыкальные инструменты, колеблющиеся детали машин, океанские приливы, переменные токи, свет, соответствующий определенной линии спектра).

2. Период этого движения не зависит от амплитуды (благодаря этому оно используется для измерения промежутков времени).

3. Это движение поддается простому математическому описанию

s= A∙sin k t

откуда следует формула

T= 2π/ k

где

k 2= (Жесткость пружины )/( Масса ).

Так можно предсказать величину Т . В других случаях измеряют Т и с помощью полученного значения подсчитывают жесткость пружины.