Эрик Роджерс - Физика для любознательных. Том 1. Материя. Движение. Сила

s= A∙sin k t

где А — амплитуда, а k — постоянная. Продифференцируем смещение s по времени t и найдем скорость, затем произведем дифференцирование еще раз и найдем ускорение

v = d s/d t= k∙A∙cos k t

a = d v/d t= — k 2A∙sin k t= — k 2 s

Отсюда видно, как вычислить период Т рассматриваемого движения:

Т= Промежуток времени от t = 0 до t = T,

= Промежуток времени, в течение которого проходит полный цикл изменения s ,

= Промежуток времени, в течение которого величина ( kt ) пробегает значения от 0 до 2π;.

т. e.

период Т= 2π/ k.

Таким образом, относительно любой системы, которой действующие на нее силы сообщают ускорение — k 2 s , можно сказать, что «эта система способна совершать простые гармонические колебания с периодом 2π/ k ».

«Формула маятника» [160]

Мы уже показали, что при малых отклонениях маятника

УСКОРЕНИЕ ГРУЗА = ( g/ L)∙ s

Сравним это с полученным выше результатом

УСКОРЕНИЕ = —k 2 s

Величина, равная в общем виде [кг], в случае маятника равна [ g / L ].

Таким образом,

Это «формула маятника», которой пользуются при точном измерении g с помощью простого маятника.

Волны

Любое изменение формы, при котором форма перемещается (но это не связано с переносом среды), называется волной . Быстро движутся волны воды, причем вода взметается вверх и опускается, а волны расходятся кругами, не унося воду далеко с собой. Понаблюдайте, как движется вверх и вниз плавающий на воде кусок пробки или поплавок, когда мимо него проходят волны. Представьте себе, как распространяются волны от веревки, рябь в пруду, звуковые волны в воздухе. От порыва ветра по некошеному полю пшеницы пробегает волна; она бежит по полю, а стебли остаются на месте, сгибаясь и снова выпрямляясь. Мы можем даже сказать, что слух в толпе тоже распространяется как волна.

Скорость, длина волны, частота

Скорость распространения волны V — это скорость, с которой перемещается ее форма, т. е. скорость перемещения любого участка волны, будь то гребень, или впадина, или область сжатия (в акустической волне).

Вдоль натянутой веревки могут перемещаться с определенной скоростью поперечные волны, и если конец веревки будет совершать простое гармоническое движение, то мы получим простую гармоническую волну с определенной длиной волны, которую обозначим греческой буквой λ (фиг. 273).

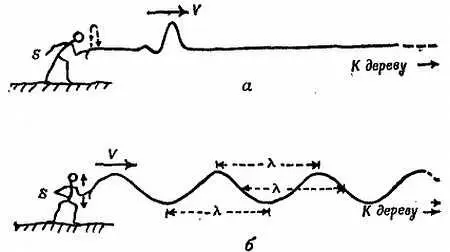
Фиг. 273. Импульс ( а) и простая гармоническая волна ( б).

Длина волны — это расстояние от гребня до гребня или от впадины до впадины, т. е. расстояние между любой парой точек, в которых состояние среды находится в одной и той же стадии ( фазе ) цикла изменений. Другими словами, это расстояние, через которое конфигурация волны повторяется.

Если источник S совершает простое гармоническое колебание и делает при этом f полных колебаний в секунду, то мы говорим, что его частота равна f . Источник S испускает волны с частотой f колебаний в секунду, и мимо любого наблюдателя О должны проходить f колебаний в секунду, иначе волны будут теряться или возникать между S и О :

ЧАСТОТА f= Число колебаний в сек,

= 1 сек / ВРЕМЯ, ЗА КОТОРОЕ СОВЕРШАЕТСЯ ОДНО КОЛЕБАНИЕ =

= 1 сек / ПЕРИОД Тсек = 1/ Т

Следовательно, для любой простой гармонической волны (как и для любого простого гармонического колебания) f= 1/ T.

Скорость распространения волн V м/сек означает, что выбранный гребень проходит V метров за одну секунду (по веревке или другой среде). Следовательно, за 1 сек от источника будет отделяться цуг волн длиной V м. Но за 1 сек источник совершает f колебаний, каждое из которых простирается на одну длину волны.

Таким образом, цуг волн длиной V м содержит f длин волн λ .

СКОРОСТЬ = ЧАСТОТА∙ДЛИНА ВОЛНЫ,

V= f∙ λ.

Это соотношение применимо к любым волнам.

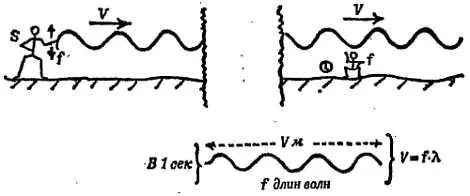
Фиг. 274. Волны.

f— Число колебаний в 1 сек.