Питер Эткинз - Десять великих идей науки. Как устроен наш мир.

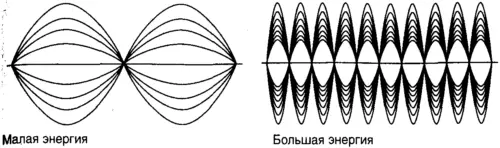
Рис. 7.9.Представление зависимости волновых функций от времени. Волновые функции осциллируют во времени со скоростью, зависящей от их энергии. Мы попытались показать, как осциллируют две волновые функции, изображенные на рис. 7.6: волновая функция с большой кинетической энергией (справа) осциллирует быстрее, чем волновая функция с малой кинетической энергией (слева).

Наконец, предположим, что мы не знаем точно энергию шарика (возможно, дрожат наши руки, держащие проволоку, или по шарику колошматят молекулы воздуха). В этом случае волновая функция не будет в точности похожа на изображенную нами, а будет суммой большого числа подобных волновых функций с несколько отличающимися формами. Результирующая суперпозиция будет волновым пакетом, похожим на изображенный на рис. 7.7. Как мы уже видели, каждая индивидуальная волновая функция осциллирует как во времени, так и в пространстве, поэтому форма, которую они образуют, складываясь вместе, меняется, ибо в один момент в одном месте гребни могут наложиться друг на друга, но затем гребень превращается во впадину, и волновой пакет принимает другую форму. Когда мы исследуем эту сумму, оказывается, что область конструктивной интерференции, создающей волновой пакет, перемещается слева направо. То есть шарик ускоряется слева направо, в точности как мы знаем из классической физики. Поэтому, когда вы наблюдаете повседневные объекты в их знакомых движениях — прыгающие мячи, летающие самолеты, гуляющих людей, — созерцайте умственным взором мысль о том, что вы наблюдаете волновые пакеты и что под их поверхностью пульсирует суперпозиция волн.

Квантовая механика делает ряд предсказаний, которые шокирующе отличаются от предсказаний классической механики, и пришло время рассмотреть эти различия. Давайте предположим, что горизонтальная проволока является короткой и что движение шарика ограничено всего несколькими сантиметрами посредством зажимов на каждом конце, как на счетах. Решающей чертой здесь является то, что допустимы только те волновые функции, которые согласуются с краевыми точками , так же как струна скрипки, зажатая в определенном месте, может совершать лишь колебания, допускаемые ее концами. Поскольку кривизна волновой функции определяется кинетической энергией шарика, а значит, его полной энергией (так как потенциальная энергия постоянна), мы заключаем, что в таком устройстве шарик может обладать только определенными энергиями. Другими словами, энергия шарика квантована , в том смысле, что она принимает дискретные значения, а не меняется непрерывно (рис. 7.10). Это общее заключение: квантование энергии , первоначально предполагаемое Планком и Эйнштейном, является следствием уравнения Шредингера и требования, чтобы волновая функция была должным образом согласована с пространством, по которому странствует частица . Вот так квантование энергии автоматически вытекает из уравнения Шредингера и так называемых «граничных условий» системы.

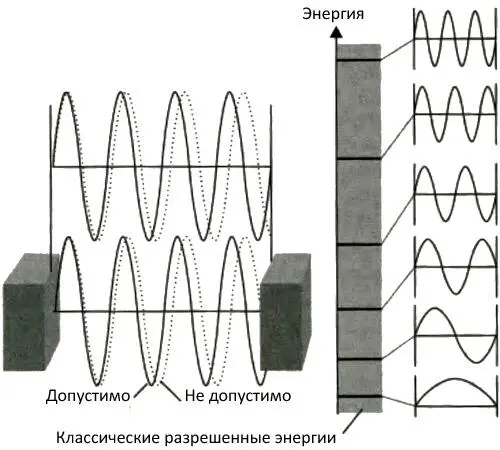
Рис. 7.10.Когда положение частицы ограничено определенной областью пространства, допустимы лишь те волновые функции (и соответствующие им энергии), которые «укладываются» в контейнер. Слева мы видим прямое изображение и изображение двух волновых функций: одна укладывается в контейнер и допустима, другая (состоящая из точек) не укладывается и не допустима. Справа мы видим результаты для энергии: серый столбик показывает классические разрешенные энергии, а горизонтальные линии показывают первые шесть квантовых, разрешенных энергетических уровней. Соответствующие волновые функции показаны правее.

Квантование интересным способом возникает в случае маятника, создавая один необычный аспект. Сначала рассмотрим волновую функцию для положения качающегося груза с точно определенной энергией (так, что он находится в определенном квантовом состоянии). Потенциальная энергия груза возрастает, когда груз отклоняется в какую-либо сторону, поэтому его кинетическая энергия падает, чтобы сохранить полную энергию постоянной, и с классической точки зрения мы можем ожидать, что волновая функция имеет наибольшую амплитуду в крайних точках качания, где груз задерживается дольше. Мы уже видели одну такую волновую функцию (рис. 7.5). Так же как для шарика между зажимами, допустимыми волновыми функциями будут те, которые согласуются с рядом величин, допускаемых качанием от одной поворотной точки до другой. Поскольку только некоторые из возможных волновых функций ведут себя подходящим образом, и каждая волновая функция соответствует определенной энергии, отсюда следует, что только некоторые энергии являются допустимыми. Оказывается, что эти допустимые энергии образуют однородную лестницу величин с разделительным интервалом между «ступеньками», который мы запишем как ħ × частота , где ħ — постоянная Планка, а частота (о которой мы скоро скажем больше) является параметром, обратно пропорциональным корню квадратному из длины маятника. Для маятника длиной 1 м на поверхности Земли вычисления дают частоту в 0,5 Гц, поэтому интервал между допустимыми энергетическими уровнями представляет собой очень маленькую и совершенно не регистрируемую величину в триста триллионно-триллионно-триллионных джоуля (3×10 − 34Дж), но он существует. Некоторые из этих энергий и соответствующие им волновые функции изображены на рис. 7.11.