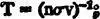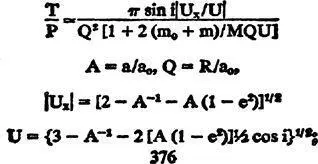Carl Sagan - Broca's Brain - The Romance of Science

Now let us imagine that the elliptical path of the comet is, in our mind’s eye, straightened out, and that it travels for some time T until it impacts a planet. During that time it will have carved out an imaginary tunnel behind it of volume σvT cm 3, and in that volume there must be just one planet.

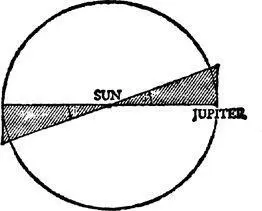
Wedge-shaped volume occupied by Velikovsky’s comet.

But 1/n is also the volume containing one planet. Therefore, the two quantities are equal and

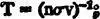
T is called the mean free time.

In reality, of course, the comet will be traveling on an elliptical orbit, and the time for collision will be influenced to some degree by gravitational forces. However, it is easy to show (see, for example, Urey, 1951) that for typical values of v and relatively brief excursions of solar system history such as Velikovsky is considering, the gravitational effects are to increase the effective collision cross section σ by a small quantity, and a rough calculation using the above equation must give approximately the right results.

The objects which have, since the earliest history of the solar system, produced impact craters on the Moon, Earth and the inner planets are ones in highly eccentric orbits: the comets and, especially, the Apollo object-which are either dead comets or asteroids. Using simple equations for the mean free time, astronomers are able to account to good accuracy for, say, the number of craters on the Moon, Mercury or Mars produced since the formation of these objects: they are the results of the occasional collision of an Apollo object or, more rarely, a comet with the lunar or planetary surface. Likewise, the equation predicts correctly the age of the most recent impact craters on Earth such as Meteor Crater, Arizona. These quantitative agreements between observations and simple collision physics provide some substantial assurance that the same considerations properly apply to the present problem.

We are now able to make some calculations with regard to Velikovsky’s fundamental hypothesis. At the present time there are no Apollo objects with diameters larger than a few tens of kilometers. The sizes of objects in the asteroid belt, and indeed anywhere else where collisions determine sizes, are understood by comminution physics. The number of objects in a given size range is proportional to the radius of the object to some negative power, usually in the range of 2 to 4. If, therefore, Velikovsky’s proto-Venus comet were a member of some family of objects like the Apollo objects or the comets, the chance of finding one Velikovskian comet 6,000 km in radius would be far less than one-millionth of the chance of finding one some 10 km in radius. A more probable number is a billion times less likely, but let us give the benefit of the doubt to Velikovsky.

Since there are about ten Apollo objects larger than about 10 km in radius, the chance of there being one Velikovskian comet is then much less than 100,000-to-1 odds against the proposition. The steady-state abundance of such an object would then be (for r = 4 a.u., and i = 1.2 0) n = (10 × 10 −5)/4 × 10 40= 2.5 × 10 −45Velikovskian comets/cm 3. The mean free time for collision with Earth would then be T = 1/(nσv) = 1/[(2.5 × 10 −45cm −3) × (5 × 10 18cm 2) × (2 × 10 6cm sec −1)] = 4 × 10 21secs 10 14years which is much greater than the age of the solar system (5 × 10 9years). That is, if the Velikovskian comet were part of the population of other colliding debris in the inner solar system, it would be such a rare object that it would essentially never collide with Earth.

But instead, let us grant Velikovsky’s hypothesis for the sake of argument and ask how long his comet would require, after ejection from Jupiter, to collide with a planet in the inner solar system. Then, n applies to the abundance of planetary targets rather than Velikovskian comets, and T = 1/[(10 −40cm −3) × (5 × 10 18cm 2) × (2 × 10 6cm sec −1)] = 10 18secs 3 × 10 7years. Thus, the chance of Velikovsky’s “comet” making a single full or grazing collision with Earth within the last few thousand years is (3 × 10 4)/(3 × 10 7) = 10 −3, or one chance in 1,000-if it is independent of the other debris populations. If it is part of such populations, the odds rise to (3 × 10 4)/10 14= 3 × 10 −10, or one chance in 3 billion.

A more exact formulation of orbital-collision theory can be found in the classic paper by Ernst Öpik (1951). He considers a target body of mass m 0with orbital elements a 0, e 0= i 0= 0 in orbit about a central body of mass M. Then, a test body of mass m with orbital elements a, e, i and period P has a characteristic time T before approaching within distance R of the target body, where

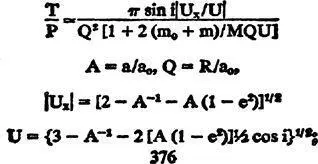
here; U is the relative velocity “at infinity” and U xis its component along the line of nodes.

If R is taken as the physical radius of the planet, then

For application of Öpik’s results to the present problem, the equations reduce to the following approximation:

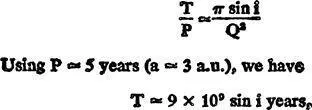
Using P 5 years (a 3 a.u.), we have

T 9 × 10 9 sin i years,

or about 1/3 the mean free path lifetime from the simpler argument above.

Note that in both calculations, an approach to within N Earth radii has N 2times the probability of a physical collision. Thus, for N = 10, a miss of 63,000 km, the above values of T must be reduced by two orders of magnitude. This is about 1/6 the distance between the Earth and the Moon.

For the Velikovskian scenario to apply, a closer approach is necessary: the book, after all, is called Worlds in Collision. Also, it is claimed (page 72) that, as a result of the passage of Venus by the Earth, the oceans were piled to a height of 1,600 miles. From this it is easy to calculate backwards from simple tidal theory (the tide height is proportional to M/r 2, where M is the mass of Venus and r the distance between the planets during the encounter) that Velikovsky is talking about a grazing collision: the surfaces of Earth and Venus scrape! But note that even a 63,000-km miss does not extricate the hypothesis from the collision physics problems as outlined in this appendix.

Finally, we observe that an orbit which intersects those of Jupiter and Earth implies a high probability of a close reapproach to Jupiter which would eject the object from the solar system before a near-encounter with Earth-a natural example of the trajectory of the Pioneer 10 spacecraft. Therefore, the present existence of the planet Venus must imply that the Velikovskian comet made few subsequent passages to Jupiter, and therefore that its orbit was circularized rapidly. (That there seems to be no way to accomplish such rapid circularization is discussed in the text.) Accordingly, Velikovsky must suppose that the comet’s close encounter with Earth occurred soon after its ejection from Jupiter-consistent with the above calculations.