Айзек Азимов - Популярная физика. От архимедова рычага до квантовой механики

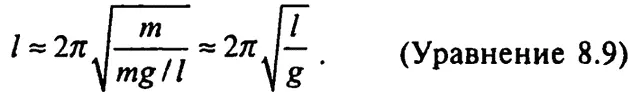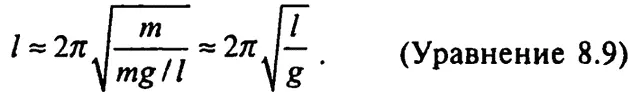
Как вы видите, период умеренно качающегося маятника не зависит от массы отвеса, а зависит (по крайней мере, в весьма хорошем приближении) от квадратного корня из длины струны, что, собственно, в далеком XVI столетии и определил Галилео экспериментальным путем.

Присутствие в уравнении величины g — ускорения, вызванного силой тяжести, — имеет очень важное значение. Если преобразовать уравнение 8.9 так, чтобы выразить значение g, то мы получим:

Это дает нам гораздо более легкий метод для измерения g, чем непосредственное измерение скорости свободного падения. Длина маятника определяется легко, и его период — также. Использование маятников во времена Ньютона показало, что изменение g в зависимости от широты местности, где производятся измерения, и добавило еще одно экспериментальное подтверждение к предположению Ньютона, что Земля имеет форму сплющенного сфероида.

Так как период умеренно качающегося маятника практически является константой, это его свойство может использоваться для измерения времени. Если маятник связан с зубчатыми колесами таким способом, что с каждым колебанием маятника колесо продвигается вперед только на один зубец, это движение тогда легко может быть преобразовано таким образом, чтобы подвинуть один указатель по кругу, составляющему точно один час (минутная стрелка), а другой указатель вокруг того же круга, но за двенадцать часов (часовая стрелка). Добавив в систему веса (гири), мы можем компенсировать затухание колебаний маятника, которое вызвано трением и сопротивлением воздуха.

Будучи уже в преклонном возрасте, Галилео имел возможность увидеть практическое применение этого его открытия, сделанного в далекой юности. Оно было осуществлено голландским ученым Христианом Гюйгенсом (1629–1695) в 1673 году. Гюйгенс не стал даже учитывать несовершенство маятника. Он показал, что физический маятник — это не математический маятник и имеет отвес некоторого конечного объема, подвешенный на струне или прутке, имеющем некую конечную массу. Он также показал, что если маятник качается по кривой, которая не является дугой окружности, а двигается по траектории гораздо более сложной кривой, называемой «циклоидой», то тогда его период будет константой. Кроме того, он показал, как можно сделать маятник, который качался бы по такой циклоидальной дуге.

С того времени использовались многие изобретательные методы, предназначенные для того, чтобы принять во внимание тот факт, что длина маятника (и поэтому его период) слегка изменяется также в зависимости от температуры окружающей среды.

Другие представители простых гармонических колебаний могут использоваться для измерения времени. Гук (тот, что открыл закон Гука) изобрел «волосок» — тонкую спиральную пружину, которая может применяться для того, чтобы развертываться и свертываться, совершая простые гармонические колебания. Работа тонкой пружины поддерживается при помощи разматывания большой «главной пружины», которую периодически подтягивают при помощи механического привода — «заводят». Такие волосковые пружины используются в наручных часах, где нет места для маятника и в которых (даже если бы место существовало) движения руки немедленно приведут маятник в беспорядочное движение [34] Но маятниковый механизм все-таки используется в наручных часах «с автоподзаводом» — там качание маятника, через систему колес, производит подтягивание главной пружины. (Примеч. пер.) .

В последние годы (конец XX века. — Пер.) для измерения времени используются колебания атомов, которые перемещаются внутри молекул в соответствии все с теми же законами простых гармонических колебаний. Такие «атомные часы» обладают гораздо большей точностью и стабильностью, чем любые из часов, которые могут быть созданы на основе механики макромира.

Я предполагал, что «тела», которые мы до этого рассматривали, были «твердыми», то есть что они являются более или менее жесткими и имеют определенную неизменяемую форму. Они сопротивляются любой силе, имеющей тенденцию к изменению или деформации этой формы (хотя если мы будем увеличивать силу без предела, то в конечном счете достигнем точки, в которой даже наиболее твердая форма будет деформироваться или ломаться). Твердые тела рассматривались как сплошные, то есть если часть твердого тела двигалась, то и все тело двигалось таким образом, чтобы сохранить свою форму.