Вернувшись домой, Галилео продолжил эксперимент, подвесив маленькие «люстры», сделанные из «отвесов» и нитей, к потолку и позволив им раскачиваться с различным периодом колебаний. (Такие подвешенные грузы называются «маятниками» (pendulum — от латинского слова, означающего «висение» или «покачивание».) Галилео смог доказать, что период колебания не зависел от тяжести отвесов, а только от квадратного корня из длины нити. Другими словами, маятник, подвешенный на нити длиной четыре фута, имеет период колебания вдвое больший, чем такой же, но с нитью длиной в один фут.
Теперь рассмотрим маятник. Если отвес висит вертикально на своей нити, он останется неподвижным. Это — его положение равновесия. Если отвес отклонить в сторону, натяжение нити заставит его двигаться по дуге круга так, что он поднимется на более высокий уровень. Если отпустить его, то под воздействием силы тяжести он будет двигаться вниз с увеличивающейся скоростью, назад по дуге круга, к своему самому нижнему положению.
Результирующая сила, которая вызывает это движение, получается в итоге сложения силы тяжести и силы натяжения нити. По мере снижения отвеса нить становится все более и более вертикальной и компенсирует все большую часть силы тяжести. Результирующая сила постоянно уменьшается по мере снижения отвеса, так же как ускорение. Когда отвес попадает в самую нижнюю часть дуги, маятник оказывается подвешенным на совершенно вертикальной линии, и нить полностью компенсирует все гравитационное напряжение. В этой точке не существует никакого неуравновешенного гравитационного напряжения и никакого ускорения. Отвес перемещается с максимальной скоростью.
Из-за инерции отвес проходит через точку равновесия и начинает описывать дугу в другом направлении. Теперь снова имеется результирующая сила, которая замедляет его движение. Чем выше он поднимается, тем больше неуравновешенная сила тяготения и тем быстрее замедляется движение отвеса. В конечном счете его движение замедляется до нуля, и в этот момент отвес достигает точки максимального смещения. Далее начинается обратное движение вниз, через точку равновесия, до максимального смещения с другой стороны и так далее.
Это очень похоже на описание простых гармонических колебаний, за исключением того, что там щипание струны вызывает движение вперед и назад по прямой линии, а смещение маятника вызывает движение вперед и назад по дуге круга. Как нам может показаться — это не является принципиальной и существенной разницей, потому что нам кажется, почему бы не существовать периодическому вращательному движению точно так, как существует периодическое поступательное движение? И действительно — имеется достаточное количество обоих видов этих простых гармонических колебаний.
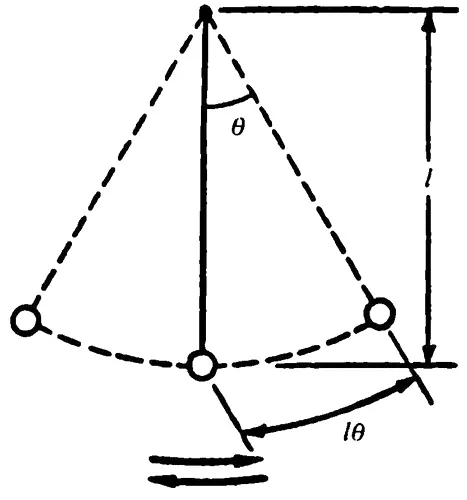
Маятник
Но действительно ли движение маятника является одним из них? Во всех случаях простых гармонических колебаний типа вибрации струны, скручивающегося и раскручивающегося шнура, движения вверх и вниз натянутой струны и раскручивания и закручивания упругой спирали сила упругости находится в пределах материала, из которого изготовлен предмет, она — производное его эластичности (упругости). В случае маятника сила упругости находится вне системы в форме неуравновешенного гравитационного напряжения. Это может представлять собой принципиальную разницу. Чтобы проверить, качается ли маятник согласно свойствам простых гармонических колебаний, мы должны проверить, действительно ли является сила упругости, компенсирующая силу тяжести, прямо пропорциональной величине смещения, что служит показателем того, что в данном случае действует закон Гука (характеризующий простые гармонические колебания).
Давайте начнем со смещения. Это — длина дуги круга, по которой маятник передвигается, чтобы достигнуть некоторого положения. Длина этой дуги зависит и от длины l струны, и от величины угла (θ) [31] Греческая буква тэта «theta» ( θ ) часто используется для представления углов.
, на который перемещается маятник. Смещение (D) фактически равно длине струны, умноженной на угол, на который перемещается вес:
D = lθ. (Уравнение 8.5)
Теперь рассмотрим силу упругости. Она, конечно, зависит от силы тяжести. Полное значение натяжения нити, вызванное силой тяжести, направленной вниз, соответственно должно быть равно mg, где m — масса отвеса, a g — ускорение свободного падения [32] На самом деле струна (нить) также имеет массу, какой бы легкой она ни была. Таким образом, мы имеем массу, распределенную по линии маятника от отвеса до центра закрепления. В каждой данной точке струна обладает некоторой массой, которая зависит от разницы в длине струны. Это также истинно и для самого отвеса, различные части которого имеют различное расстояние от точки закрепления. В идеальном варианте маятник должен состоять из массивного отвеса с нулевым объемом, приложенным невесомой струной к центру закрепления. Такое устройство называется «идеальным или простым маятником» и, естественно, в реальном мире не существует. Однако, используя тяжелый отвес и легкую струну, можно сделать реальный маятник, который по своим свойствам будет приближен к идеальному маятнику. (У нас это называется «математическим» и «физическим» маятниками соответственно.) (Примеч. пер.)
. Однако отвес не двигается точно вниз, он перемещается по дуге. Это перемещение складывается из воображаемых «скатываний» по наклонной плоскости, которая изменяет свой угол наклона в каждой из точек окружности.
Читать дальше













