Яков Гегузин - Живой кристалл

Если принять описанную модель роста и если считать, что время ожидания появления жизнеспособного зародыша τзначительно больше времени, в течение которого он разрастается, то легко написать основную формулу теории, определяющую скорость роста кристалла:

υ кр= a/τ

где а — расстояние между атомами, т. е. толщина одноатомного слоя.

Теоретики сумели вычислить величину τ, нашли ее связь со степенью неравновесности, т. е. со степенью переохлаждения расплава или пересыщения раствора (источника атомов, питающих кристалл). Выяснилось, что т увеличивается по мере уменьшения степени неравновесности, стремясь к бесконечности при стремлении степени неравновесности к нулю. И скорость при этом стремится к нулю.

Все оправданно, разумно, и, казалось бы, эксперимент не должен, не имеет права противоречить такой стройной логичной теории. Природа, однако, оказалась изощреннее формально строгой логики теоретиков. Выяснилось, что во многих случаях при малой степени неравновесности среды реальные кристаллы растут существенно быстрее, чем это предсказывает логически стройная теория. Существенно — это значит не в 2—3 раза, а в тысячи раз. Теория явно нуждается в коренном усовершенствовании, дисциплинированная логика явно где-то ограничила фантазию, и правда ускользнула от теоретиков.

Итак, теория встретилась с трудностью — залогом того, что не за горами ее усовершенствование. Оно появилось на кончике пера английского теоретика Франка, размышлявшего о структуре реального кристалла менее дисциплинированно, чем его предшественники. Он усмотрел слабую сторону теории Косселя и Странского в том, что, согласно их представлениям, идеальный зародыш разрастается в идеальный кристалл. Ни в зародыше, ни в кристалле нет дефектов, кристалл растет так, что на его поверхности наслаиваются идеальные атомные плоскости. Именно для этого Косселю и Странскому понадобился идеальный зародыш, который долго не желает появляться, если степень неравновесности невелика. Франк, однако, видел перед собой реальный кристалл, и его логика, очевидно, развивалась следующим образом. От двумерного зародыша надо отказаться. Если даже при очень малой степени неравновесности кристалл растет быстро, на его поверхности, видимо, существует не исчезающая в процессе роста ступенька, к которой пристраиваются одиночные атомы. В этом месте своих рассуждений Франк освободился от гипноза предшественников и высказал неожиданный фантастический домысел: неисчезающая ступенька. В теории Косселя и Странского роль ступеньки играет контур зародыша.

Но в этом случае ступенька должна появиться, разрастись и исчезнуть, когда слой полностью достроится. А по мысли Франка, такая ступенька должна быть всегда, не исчезая в процессе роста. Он предположил, что такая ступенька на поверхности есть следствие дефекта объема кристалла. Этот дефект Франк назвал винтовой дислокацией. Именно Франк поселил в кристалле винтовую дислокацию.

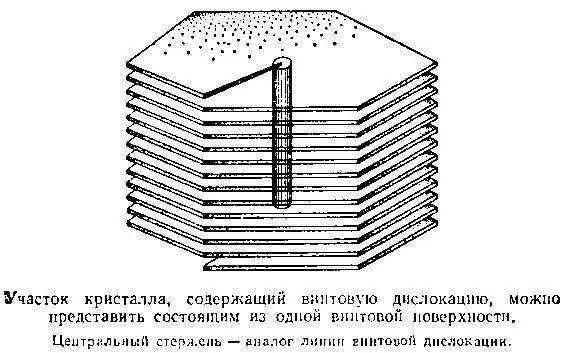
Проще всего представить себе винтовую дислокацию как некую линию, вокруг которой наслаивается кристалл в виде одной-единственной плоскости, подобно винтовой лестнице. Винтовая лестница часто «навинчивается» на центральный стержень. Вот его и следует считать моделью линии винтовой дислокации. Ступенька на поверхности — это обрыв атомной плоскости, накручивающейся вокруг линии винтовой дислокации. Чуть курьезно говоря, согласно Франку, кристалл, содержащий одну винтовую дислокацию, состоит из одной плоскости. Именно она и достраивается в процессе роста. Согласно Косселю и Странскому, плоскости зарождаются и завершают свой рост; согласно Франку, все время растет одна и та же плоскость. У Косселя и Странского — слоистый рост, у Франка — спиральный. Когда степень неравновесности велика, может осуществляться и механизм слоистого роста, а вот когда она мала — помирить эксперимент с теорией может лишь механизм спирального роста.

Мысль теоретика, родившего образ винтовой дислокации, многим вначале показалась фантастической и вызвала к себе настороженное отношение: фантазия, разумеется, необходима для развития науки, но фантазия должна иметь предел.