Юрий Черноскутов - Логика. Краткий конспект

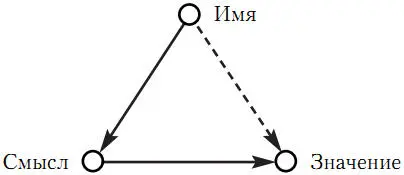
Рис. 1.1

Тот факт, что один и тот же предмет может обозначаться разными именами, возможен благодаря тому, что эти имена имеют одинаковые значения, но разные смыслы. Поэтому, считает Фреге, различение смысла и значения позволяет объяснить, почему мы можем ставить знак равенства в выражении «А = В», хотя А и В суть разные вещи. Мы вправе делать это тогда, когда А и В имеют одинаковые значения, несмотря на то что они имеют разные смыслы. Больше того, на этом основании мы вправе заменять А и В друг на друга, сохраняя при этом уверенность, что значение более сложного выражения, в рамках которого производится такая замена, не изменится.

Эта теория становится особенно продуктивной, если мы вслед за Фреге распространим ее на предложения. Фреге рассматривал последние как частный случай имен. Смыслом предложения он счел выражаемую им мысль, или то, что в логике обычно называется суждением, а вот значением – его истинностное значение, истину или ложь. Эта теория стала очень резонансной и широко обсуждаемой, причем не только в логике. Здесь мы отметим лишь, что она позволяет обосновать принципы дедуктивных переходов между высказываниями, выраженными в некотором языке. Мы можем переходить от высказывания А к высказыванию В на том основании, что они имеют одинаковые значения, будучи при этом различными по смыслу. Таким образом, понятие смысла как бы выносится за скобки, оно не принимается во внимание; логические связи и отношения устанавливаются и изучаются только на основе значения языковых выражений. По крайней мере, в классической логике дела обстоят именно так.

Существуют, тем не менее, контексты, в которых замена одного предложения на другое на том основании, что они имеют одинаковые значения, недопустимо. Например, в предложении «Колумб считал, что земля шарообразна» входящее в него предложение «Земля шарообразна» нельзя заменить на предложение «Петербург – город на Неве», хотя оба они имеют значение «истина». Ведь тогда вместо истинного исходного предложения мы получим ложное. В таких контекстах приходится принимать во внимание смыслы выражений. Подобного рода контексты называются интенсиональными , и их исследования осуществляются в рамках неклассических логик.

Надо сказать, что, когда мы пытаемся прилагать эту теорию к определенным видам имен, в нее приходится вносить изменения. Возьмем, например, собственное имя. Собственным именем называется имя, которое предназначено для указания на один, и только один объект. Многие собственные имена, которые мы встречаем в повседневной жизни, не удовлетворяют этому определению, т. е. они не являются собственными в логическом смысле. Действительно, возьмем ли мы имена или фамилии людей, клички животных, нередко даже названия населенных пунктов – эти имена, как правило, обозначают более чем один объект. Логические же собственные имена – это имена уникальных объектов, это своего рода ярлыки, которые приклеиваются к вещам: одна вещь – один ярлык. Обозначение объекта с помощью собственного имени можно уподобить указанию на него пальцем: в последнем случае мы не сообщаем о предмете никакой информации, мы только указываем на него. Исходя из подобных соображений Б. Рассел утверждал, что собственное имя имеет значение, но не имеет смысла.

Следующий вид имен – общие имена . Общими называются имена, предназначенные для указания на произвольный объект определенной области. Примерами общих имен могут служить такие имена, как «человек», «число», «закон». Для них уже сам Фреге усложнил свою схему. Он полагал, что эти имена указывают на объект не напрямую, но посредством такой сущности, как понятие . Именно понятие, по его мнению, является значением общего имени. Под понятие, в свою очередь, подпадают определенные объекты. При этом число объектов, подпадающих под понятие, может изменяться от нуля до бесконечности. Взаимосвязь общего имени с указанными компонентами иллюстрируется на рис. 1.2.

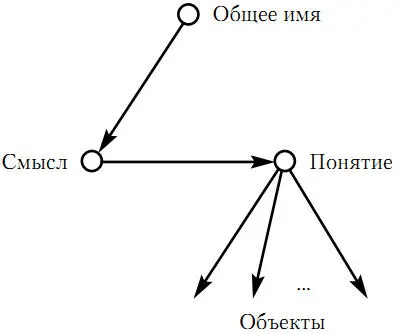
Рис. 1.2

Тем не менее, каковы бы ни были особенности этой теории применительно к различным видам имен, для всех них в классической логике имеют силу следующие принципы употребления имен:

1) всякое имя является именем предмета;