Существует важная операция, называемая скалярным произведением (или внутренним произведением) двух векторов, которая может быть использована для того, чтобы очень просто выразить такие понятия, как «единичный вектор», «ортогональность» и «амплитуда вероятности». (В обычной векторной алгебре скалярное произведение равно ab cos v , где а и b — длины векторов, a v — угол между их направлениями.) Скалярное произведение векторов из гильбертова пространства дает комплексное число. Скалярное произведение двух векторов состояния | ψ ) и | X ) записывается в виде | ψ | X ). Для него справедливы алгебраические правила
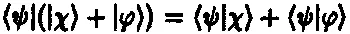 ,
,
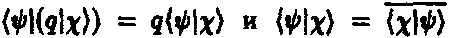
где черта сверху означает комплексное сопряжение. Числом, комплексно сопряженным с z = х + iy , называется 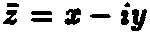
, где х и у — действительные числа; обратите внимание на то, что
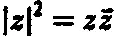 .
.
Ортогональность векторов состояния | ψ ) и | X ) записывается в виде соотношения
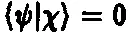
Квадрат длины вектора состояния | ψ ) есть величина
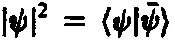
поэтому нормировки | ψ ) к единичному вектору представимо в виде
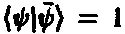
Если «акт измерения» вызывает скачкообразный переход состояния | ψ ) либо в состояние | X ), либо во что-то, ортогональное | X ), то амплитуда этого скачкообразного перехода в состояние | X ) равна ( X | ψ ) в предположении, что | ψ ) и | X ) нормированы. Без нормировки вероятность скачкообразного перехода из | ψ ) в | X ) можно представить в виде
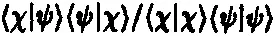 (См. Дирак [1947].)
(См. Дирак [1947].)
Для тех, кто знаком с операторным формализмом квантовой механики, это измерение (в обозначениях Дирака) определяется ограниченным эрмитовым оператором | X )( X |. Собственное значение 1 (для нормированного | X )) означает ДА, а собственное значение 0 — НЕТ. (Векторы ( X |, | ψ ) и т. д. принадлежат гильбертову пространству, дуальному к исходному.) См. фон Нейман [1955], Дирак [1947].
От английского spin — «вращение». — Прим. ред.
В предыдущем описании квантовой системы, состоящей из одной частицы, я прибег к сверхупрощению, проигнорировав спин и предположив, что состояние может быть описано заданием одного лишь пространственного положения. Действительно, существуют некоторые частицы, называемые скалярными , их примерами могут служить ядерные частицы, известные под названием пионов ( π -мезоны, см. гл.5 «Масса, материя и реальность»), или некоторые атомы, для которых спин оказывается равным нулю. Для таких (и только для таких) частиц приведенное выше описание в терминах одного лишь пространственного положения действительно будет достаточным.
Здесь и выше я предпочел не загромождать формулы множителями типа 1 / √2 , которые нужны, если мы требуем, чтобы векторы |→)и |←)были нормированными.
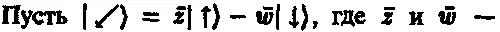 комплексно сопряженные чисел ω и z . (см. прим.151)
комплексно сопряженные чисел ω и z . (см. прим.151)
Существует стандартная экспериментальная установка, известная как прибор Штерна-Герлаха, которую можно использовать для измерения спинов атомов. Атомы выпускаются в пучок, который проходит в сильно неоднородном магнитном поле, направление неоднородности которого задает направление, в котором производится измерение спина. Пучок расщепляется на два (для атома со спином 1 / 2 или на большее число частей — для атома с бо́льшим спином), один пучок дает атомы с ответом ДАна измерение спина, а другой — атомы с ответом НЕТна измерение спина. К сожалению, по некоторым техническим причинам, не имеющим отношения к интересующим нас вопросам, такой прибор не может быть использован для измерения спина электрона, и поэтому приходится прибегать к косвенной процедуре (см. Мотт, Мэсси [1965]). По этой и по другим причинам я предпочитаю не вдаваться в подробности относительно того, как в Действительности измеряют спин электрона.
Читать дальше

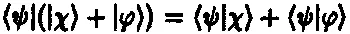 ,
,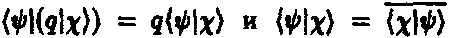
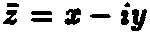
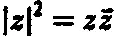 .
.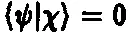
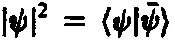
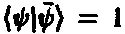
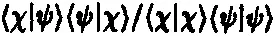 (См. Дирак [1947].)
(См. Дирак [1947].)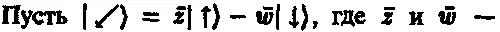 комплексно сопряженные чисел ω и z . (см. прим.151)
комплексно сопряженные чисел ω и z . (см. прим.151)