Роджер Пенроуз: Новый ум короля: О компьютерах, мышлении и законах физики

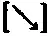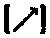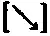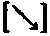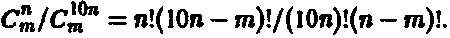
такой же, как между [→] и

,

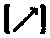то вероятность согласия между исходами P- измерений и новых Е- измерений (обозначим их, например, E'- измерениями ) по-прежнему была бы лишь немного меньше 15 %. С другой стороны, если E- настройка была бы [→], как прежде, а Р- настройка была бы

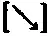
а не

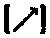
то серия Е- результатов осталась бы такой же, как прежде, а новая серия Р- результатов , которую мы обозначим, например, Р', была бы в согласии лишь немногим меньше 15 % с исходной серией Е- результатов . Отсюда следует, что согласие между Р'- измерением и Е' — измерением могло бы быть не выше 45 % (= 15% + 15% + 15%), если бы эти измерения производились бы, соответственно, при настройках

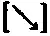
и [↑]. Но угол между

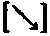
и [↑] равен 135 °, а не 45 °, поэтому вероятность согласия должна была бы быть чуть больше 85 %, а не 45 %. Это — противоречие, показывающее, что допущение, согласно которому выбор измерения, произведенного Е- измерителем , не может влиять на результаты Р- измерений ( и наоборот ) должно быть ложно! За этот пример я признателен Дэвиду Мермину. Вариант, приведенный в тексте, заимствован из его статьи (Мермин [1985]).

Более ранние результаты, принадлежавшие Фридману и Клаузеру [1972], основаны на идеях, высказанных Клаузером, Хорном, Шимони и Холтом [1969]. В этих экспериментах все еще имеется один спорный пункт в связи с тем, что используемые в экспериментах детекторы фотонов обладают КПД, существенно меньшим 100 %, поэтому лишь сравнительно малая доля испущенных фотонов оказывается реально детектированной. Однако даже с такими детекторами согласие с квантовой теорией столь совершенно, что трудно понять, как повышение КПД детекторов способно внезапно ухудшить согласие с теорией!

Однако между отдельным фотоном и электромагнитным полем существует важное различие в типе допустимых решений уравнения. Классические максвелловские поля с необходимостью действительнозначные , тогда как состояния фотона комплекснозначные. К тому же фотон должен удовлетворять так называемому условию «положительной частоты».

Кажется, что квантовая теория поля дает некоторый простор для невычислимости. (См. Комар [1964].)

Некоторые «ревностные поборники» релятивизма могли бы предпочесть использовать световые конуса наблюдателей, а не их пространства одновременных событий. Однако, все сделанные нами заключения от этого не изменятся.

После первого просмотра напечатанного варианта мне вдруг пришло в голову, что оба человека должны были умереть задолго до этого. «Сопоставить свои наблюдения», в принципе, могли бы их отдаленные потомки (до которых вся информация о возникшем когда-то споре дошла бы, передаваясь из поколения в поколение).

В общем случае n , m вероятность равна

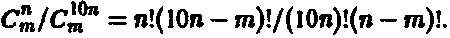
Используемый здесь логарифм называется натуральным, т. е. берется по основанию

е = 2,7182818285 …,

а не по основанию 10 , однако это различие в нашем случае совершенно несущественно. Натуральный логарифм, x = log n , числа n — это степень, в которую мы должны возвести е , чтобы получить n , т. е. решение уравнения e x = n (см. ссылку 62).

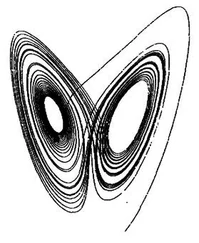
Было бы, конечно, неверным утверждать, что наша точка фазового пространства вообще никогда не достигнет ни одной из предшествующих областей меньшего объема. Если мы подождем достаточно долго, точка может снова оказаться внутри одного из них, несмотря на его ничтожно малый объем (в соответствии с теоремой о возвращении Пуанкаре .) Однако, в подавляющем большинстве случаев, соответствующие масштабы времен будут чудовищно велики, порядка