В частности, Дж. Дж. Бальмер отметил в 1895 году, что частоты спектральных линий водорода удовлетворяют формуле R ( n -2— m -2 ), где n и m — положительные целые числа ( R — постоянная).
Возможно, нам не следовало бы слишком легко отказываться от этой «чисто полевой» картины. Эйнштейн, который (как мы увидим в дальнейшем) глубоко сознавал дискретный характер квантовых частиц, провел последние тридцать лет своей жизни, пытаясь построить более общую теорию такого классического типа. Но попытки Эйнштейна, как и все прочие попытки, оказались тщетными. По-видимому, для объяснения дискретной природы частиц необходимо что-то еще помимо классического поля.
Это наблюдение необходимо произвести так, чтобы не помешать прохождению частицы через щель t . Этого можно было бы достичь, разместив детекторы в другом месте — рядом с щелью s . Тогда можно будет делать заключение о прохождении частицы через щель t , когда эти детекторы не срабатывают!
Здесь возникает техническая трудность, так как настоящая вероятность найти частицу строго в данной точке была бы равна нулю. Поэтому величину
| ψ ( x )| 2 мы предпочитаем называть плотностью вероятности . Это означает, что на самом деле нам нужна вероятность найти частицу в некотором малом интервале фиксированных размеров. Таким образом, ψ ( х ) определяет плотность амплитуды , а не просто амплитуду.
На стандартном аналитическом языке любая из наших штопорообразных винтовых линий (т. е. любое импульсное состояние) задается формулой
ψ = e ipx/h = cos (ipx/h) + i sin (ipx/h),
где р — рассматривемое значение импульса z . (см. главу 3)
Эти две эволюционные процедуры были описаны в классическом труде выдающегося американского математика венгерского происхождения Джона (Яноша) фон Неймана [1955]. Его «процесс 1» — то, что я назвал R-процедурой — «редукцией вектора состояния», а его «процесс 2» — то, что я назвал U-процедурой — «унитарной эволюцией» (унитарность означает, что амплитуды вероятности в ходе эволюции сохраняются). На самом деле существуют и другие (хотя и эквивалентные) описания эволюции Uквантового состояния, в которых не используется термин «уравнение Шредингера». Например, в « картине Гейзенберга » состояние описывается таким образом, что кажется, будто оно вообще не эволюционирует; динамическая эволюция понимается как непрерывный сдвиг смысла координат положения/импульса. Разные отличия этих картин для нас сейчас несущественны, так как описания процесса Uполностью эквивалентны.
В более обычном квантовомеханическом описании эту сумму следовало бы разделить на нормирующий множитель, равный √2, т. е. взять сумму ( ψ t + ψ b ) ∕ √2, но усложнять таким образом описание сейчас нет необходимости.
Это важное понятие бесконечномерного пространства, с которым нам уже приходилось встречаться в предыдущих главах, ввел Давид Гильберт задолго до открытия квантовой механики и для совершенно других математических целей!
Для полноты следовало бы также привести все требуемые алгебраические правила, записанные в используемых в тексте обозначениях (Дирака),
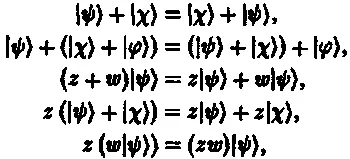
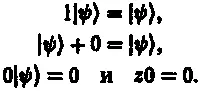
Угловые скобки, использованные в книге,
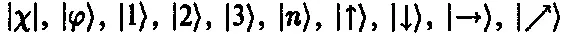 , заменены на круглые
, заменены на круглые
| x |, | ψ ), | 1 ), | 2 ), | 3 ), | n ), | ↑), | ↓),|→),|←) — за отсутствием в «таблице символов». В элементах изображений (при ипользовании картинок), соответственно, осталось все как есть. Надеюсь, путанницы не возникнет. — Прим верст. fb2
Не исключается также и случай, когда эта комбинация представляет собой бесконечную сумму векторов. Полное определение гильбертова пространства (которое, на мой взгляд, слишком формально для того, чтобы здесь вдаваться в его подробности) включает в себя правила, позволяющие оперировать с такими бесконечными суммами.
Читать дальше

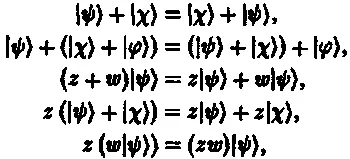
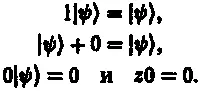
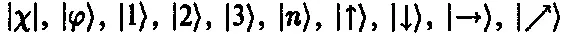 , заменены на круглые
, заменены на круглые