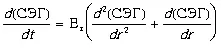 . (3.1)
. (3.1)
Из данной модели видно, что если часть второго слагаемого в скобках мала, то решение уравнения отвечает нормальному гауссовскому закону распределения, которое соответствует обычному механизму диффузии:
СЭГ 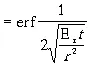 , (3.2)
, (3.2)
в противном случае имеет место иная функция распределения.
Напрашивается вопрос, какому закону распределения соответствует решение уравнения (3.1), если в математической лингвистике известно [14], что закон (3.2), т.е. нормальное распределение, соответствует описанию поведения системы со «стертой» семантикой, отсутствию дискурсии? Следовательно, поведенческая динамика СЭГ по закону (3.2) не может приводить к выживанию.
Если же поведенческая динамика СЭГ при заданном Е тпредставляет собой ряд «творческих импульсов», эффект которых зависит, с одной стороны, от их интенсивности, а с другой, от величины r , созданных действием предыдущих импульсов, то в этом детерминированном случае решением закона (3.1) является логнормальное распределение с Е т= 1 в виде:
СЭГ = 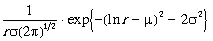 , (3.3)
, (3.3)
где m — среднее значение r , s — среднеквадратичное отклонение.
Логнормальность «словаря и текста» отражает присущий языку [5], т.е. мышлению, принцип оптимального кодирования информации. В отличие от закона (3.2) закон логнормального распределения следует принять для СЭГ за основу «творческого выживания». При этом, полагая, что для векторного равенства
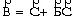
по модулю 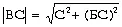 , то, не нарушая общей концепции социологии, закон (3.3) следует признать необходимым и достаточным для выживания СЭГ как группы творческих возможностей, следующих в форме отдельных импульсов. Аналогия между творческими возможностями группы СЭГ, с одной стороны, и оптимальным кодированием информации, присущим естественному языку как форме мышления, с другой, представляется фундаментальной. Возможно, что в фундаменте структуры языка лежит не только сложность мышления (гипотеза Сепира–Уорфа), но и сложность задач, подлежащих решению СЭГ при поиске способа выживания.
, то, не нарушая общей концепции социологии, закон (3.3) следует признать необходимым и достаточным для выживания СЭГ как группы творческих возможностей, следующих в форме отдельных импульсов. Аналогия между творческими возможностями группы СЭГ, с одной стороны, и оптимальным кодированием информации, присущим естественному языку как форме мышления, с другой, представляется фундаментальной. Возможно, что в фундаменте структуры языка лежит не только сложность мышления (гипотеза Сепира–Уорфа), но и сложность задач, подлежащих решению СЭГ при поиске способа выживания.
Если полученный результат модельно-гносеологического анализа категории выживания СЭГ действителен, то, по крайней мере, следует ожидать, что в такой деликатной области, как финансово-экономическая, где проблема технологии производства и ее выживание тесно связаны с финансами, экономикой, можно надеяться получить подтверждение закона выживания (3.3), анализируя классическую форму финансово-экономических расчетов:
PT № MV + Mў Vў, (3.4)
где P — уровень цен, T — количество товаров и услуг, M — количество денег, V — скорость их обращения, Mў — количество ценных бумаг, Vў — скорость их обращения.
3.2. Рефлексия «финансово-экономического выживания»
Откажемся от линейного вида закона (3.4), хотя, как известно, эта классическая закономерность считается открытой еще в XVIII в. Более того, путем рефлексивного метода [32] найдем новые закономерности между параметрами P , T , MV , Mў Vў для ситуации, когда между финансово-экономическими возможностями h в m случаях (порядок относительного обращения ценностей) и видами технологий q , реализуемых в n вариантах, имеет место равновесие в форме равномощности множеств:
nn = mh . (3.5)
Введем понятие относительного обращения c = MV / Mў Vў как отношения массы денег и скорости их обращения к массе ценных бумаг и скорости их обращения. Тогда уравнение состояния финансово-экономических возможностей будет: h = h ( P , T , c ). Будем характеризовать уровень технологии n = n ( с ), где с — константа скорости конверсии финансово-экономических возможностей системы в заданный уровень технологии или наоборот. По аналогии, например, с известным «законом действия масс» в химии, т.е. заимствуя семиотические возможности «языка химии», будем полагать, что уровень цен P — величина, обратная покупательной силе денег, прямо пропорционален относительному обращению ценностей c в степени порядка m обращения ценностей:
Читать дальше

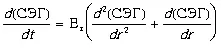 . (3.1)
. (3.1)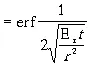 , (3.2)
, (3.2)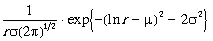 , (3.3)
, (3.3)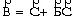
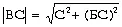 , то, не нарушая общей концепции социологии, закон (3.3) следует признать необходимым и достаточным для выживания СЭГ как группы творческих возможностей, следующих в форме отдельных импульсов. Аналогия между творческими возможностями группы СЭГ, с одной стороны, и оптимальным кодированием информации, присущим естественному языку как форме мышления, с другой, представляется фундаментальной. Возможно, что в фундаменте структуры языка лежит не только сложность мышления (гипотеза Сепира–Уорфа), но и сложность задач, подлежащих решению СЭГ при поиске способа выживания.
, то, не нарушая общей концепции социологии, закон (3.3) следует признать необходимым и достаточным для выживания СЭГ как группы творческих возможностей, следующих в форме отдельных импульсов. Аналогия между творческими возможностями группы СЭГ, с одной стороны, и оптимальным кодированием информации, присущим естественному языку как форме мышления, с другой, представляется фундаментальной. Возможно, что в фундаменте структуры языка лежит не только сложность мышления (гипотеза Сепира–Уорфа), но и сложность задач, подлежащих решению СЭГ при поиске способа выживания.



![Сергей Кутолин - Зяма Пешков - легионер и бригадный генерал [рефлексия жизнеописания]](/books/422558/sergej-kutolin-zyama-peshkov-thumb.webp)
