Однако, естественно, не вся PGL – J -система, т.е. интеллектуальная система, конвертируемая в максимально полезную работу, есть вектор, творческий энтузиазм Е т. Часть PGL – J -системы должна обладать диссипацией, рассеянием. Какова же «гистология» этой части? В отличие от PGL – J -системы как банка творческих идей диссипация J -системы есть произведение численного многообразия мнений, теории ( M ) и информации ( Jnf ), усвоенной интеллектуальной системой ( J -системой) в процессе творческого акта. Естественно, что усвоенная информация ( Jnf ) есть логарифмическая мера вероятности от всей без исключения собранной информации творчества субъектов. Отсюда диссипация J -системы ( JD ) есть произведение MJnf , т.е. часть интеллектуальной системы, составляющая ее уровень от PGL – J -системы, который не реализуется в творческий энтузиазм, а рассеивается на интересе к смежным областям творчества и не проявляется в векторе конкретного творческого энтузиазма (E т), откуда Е т= B + П = PGL - J – MJnf . Таким образом, интеллектуальная система ( PGL – J ) может быть представлена конусом, образующие которого сходятся в вершине (результате творчества), обегая площадь рассеяния интеллекта ( JD ). Чем больше площадь рассеяния интеллекта, чем меньше величина творческого энтузиазма Е т, тем короче высота конуса как меры вдохновения [22]. Связи между категориями J -системы, выраженными символами Е т, J , JD , есть символическая модель интеллекта, и, по крайней мере, не менее общая, чем та, которой пользуются, например, в экономике при оценке покупательной силы денег [30]. Можно далее показать, что не только символическая, но и аналитическая модель может быть получена путем рефлексии, при анализе, например, выборной кампании ... народных депутатов в Верховный Совет СССР в Новосибирской области.
2.2. Рефлексия аналитической модели выборов народных депутатов в Верховный Совет СССР в Новосибирской области и по округу №21 РСФСР.
Будем полагать, что в основе такой рефлексии лежит взаимодействие не более чем двух неантагонистических коллективов, план «боевых» действий которых включает миниколлективы, работающие в рамках двоичной или многозначной логики, что соответственно характеризуется параметрами а = 2 и b = 3. Следует отметить, что модели «боевых действий» неантагонистических коллективов Ланчестера–Рашевского рассматривались в литературе неоднократно [12, 31] в форме линейных дифференциальных уравнений. Поэтому приведем окончательный результат таких уравнений в виде:
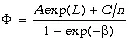 , (2.1)
, (2.1)
где F — общая численность лиц, принявших участие в голосовании; C / n — число недействительных бюллетеней, приходящихся на каждого из двух кандидатов. Эта единственная постоянная величина в данной модели сложного экспоненциального типа может быть определена по данным хотя бы одного из избирательных округов. В среднем (8–12% отн. ошибки) C / n = 3927. Тогда указанная модель имеет вид:
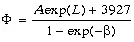 . (2.2)
. (2.2)
В числителе этой дроби величина A exp( L ) — теоретически соответствует численности голосов избирателей, поданных «за» депутата, а в знаменателе величина [1 – exp(–b )] — числу голосов, поданных «против» депутата.
Определим смысл величин A , L , b, как функции поведения коллектива с параметрами a = 2 и b = 3, т.е. параметрами, соответствующими двузначной и многозначной логике поведения.
Пусть есть доля информации о положительных качествах претендента в депутаты. Естественно, что такая доля может быть и более и менее 100%, но, принимая во внимание параметры b и а , можно определить разумно величину b = b / а 2, и тогда, действительно, b может быть в среднем больше или меньше 3/4. Пусть L в отличие от b есть уровень информации, равный объему информации, получаемому минимальным коллективом поддержки A , и складывающийся только из ситуаций, характеризуемых двоичной логикой, т.е. L = а 3= 2 3= 8. Определим минимальную величину коллектива поддержки депутата A как коллектив, в котором депутаты обязаны действовать в целях успеха не иначе как по принципу многозначной логики, согласно которому b = 3. Тогда, по определению, во всяком случае A = b 3= 27. Итак, путем цепи суждений мы теоретически оценили параметры модели выборов как величины, равные A теор= 27, b теор= 3/4, L теор= 8. Сама же аналитическая модель выборов как часть рефлексии есть умозаключение, т.е. новое знание, которое можно проверить. Действительно, если параметры A , L , b, будучи подставлены в модель, совпадут по своим средним значениям между собой и с соответствующими результатами экспериментальных данных по голосованию, т.е. величинами голосов «за», «против», общей численностью избирателей, принявших участие в голосовании, то предпринятая рефлексия есть фактически реализованное умозаключение. Результаты таких расчетов приведены в табл. 2.2 (фамилии избранных депутатов Верховного Совета СССР подчеркнуты).
Читать дальше

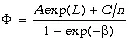 , (2.1)
, (2.1)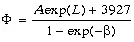 . (2.2)
. (2.2)



![Сергей Кутолин - Зяма Пешков - легионер и бригадный генерал [рефлексия жизнеописания]](/books/422558/sergej-kutolin-zyama-peshkov-thumb.webp)
