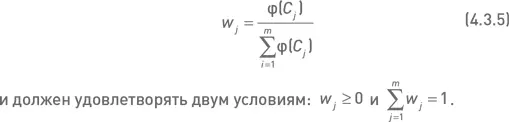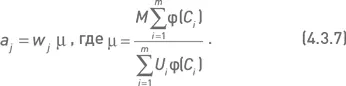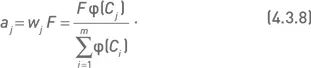Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

Независимо от вида функции φ( С ), вес j -й комбинации в составе портфеля определяется как:

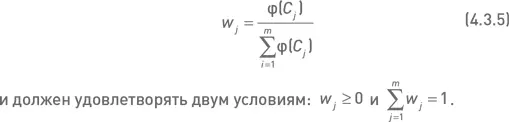
Способ вычисления количества экземпляров комбинации C j в портфеле зависит от подхода, применяемого на первом уровне системы управления капитала. Если капитал, выделяемый для инвестирования в опционный портфель, представляет собой объем средств, который потребуется в будущем при исполнении опционов, то такой капитал является суммарным эквивалентом портфеля M (см. описание в предыдущем разделе). В этом случае количество экземпляров комбинации может быть рассчитано по формуле

или, что то же самое, но с помощью константы μ:

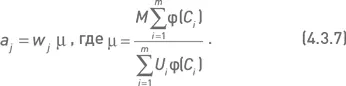
Если выделяемый для инвестирования капитал F представляет собой суммарный объем инвестиций в опционный портфель (например, суммарный объем маржевых требований по всему портфелю), то количество экземпляров комбинации С j определяется по формуле

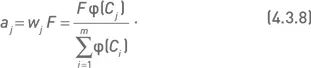
В дальнейших исследованиях мы будем использовать подход, основанный на суммарном эквиваленте портфеля (формула 4.3.7).

Эти два показателя, рассчитываемые на основе заданного распределения, представляют собой критерии оценки опционных комбинаций. Для простоты мы будем использовать логнормальное распределение. Математическое ожидание прибыли, рассчитанное на основе логнормального распределения, будем обозначать EPLN. Вероятность получения прибыли, рассчитанную на основе логнормального распределения, будем обозначать PPLN. Подробное описание и алгоритмы расчета этих показателей приводятся в нашей книге «Опционы: системный подход к инвестициям».

Оба показателя являются позитивными – большие значения показателей соответствуют более привлекательным комбинациям. Весовая функция φ( С ) для j -й комбинации принимает значение показателя, соответствующее этой комбинации. В таблице 4.3.2 показаны значения критериев и соответствующие им значения весов, рассчитанные с помощью формулы 4.3.5. Примеры, приведенные в таблице, используют те же опционные комбинации, которые рассматривались в разделе 4.3.1.

Для расчета количества экземпляров каждой комбинации в составе портфеля необходимо воспользоваться формулой 4.3.7. Для примера вычислим вес и количество экземпляров комбинации, относящейся к акции CAT, для случая когда капитал распределяется по критерию «математическое ожидание прибыли». Из таблицы 4.3.2 следует, что Σφ( C i ) = 0,1196. Используя данные таблицы 4.3.1 для цен акций, можно рассчитать Σ U i φ( C i ) = 11,338. Принимая M = 1 000 000, получаем:

Учитывая, что для акции CAT φ( С 4 ) = 0,001, вычисляем вес w 4 = 0,001: 0,1196 = 0,0085 и число экземпляров комбинации. a 4 = 10 550 × 0,0085 = 89,78. Используя этот же алгоритм расчета, легко показать, что при распределении капитала по критерию «вероятность прибыли» вес данной комбинации составит w 4 = 0,472, а количество экземпляров a 4 = 580,01.

Дельта опциона выражает чувствительность цены опциона к изменениям стоимости базового актива. Для опционов, относящихся к одному базовому активу, дельта является аддитивной величиной. Поэтому дельта комбинации равна сумме дельт отдельных опционов. Дельта опциона колл принимает значения от 0 до 1, а дельта пута находится в диапазоне от −1 до 0. Соответственно, для одного стрэддла дельта может принимать значения от −1 до 1. Поскольку в наших примерах рассматриваются портфели, состоящие только из коротких стрэддлов, нейтральность комбинаций к поведению базового актива является в целом благоприятным фактором. Это означает, что чем ближе дельта комбинации к нулю, тем менее рискованной является позиция. Следовательно, при распределении капитала абсолютная величина дельты является «негативным» показателем. Поэтому мы зададим весовую функцию в следующем виде: φ( C ) = 1 – |δ( C )|, где δ( C ) – дельта комбинации C .