Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

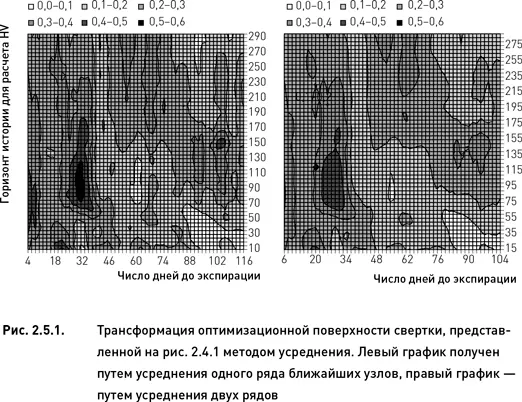
Применим данную процедуру к оптимизационной поверхности, полученной ранее в результате свертки трех целевых функций. Исходное оптимизационное пространство (рис. 2.4.1) содержит три оптимальные области, каждая из которых может рассматриваться в качестве кандидата на поиск оптимального решения. На рис. 2.5.1 показаны две трансформации оригинальной поверхности, построенные для m = 1 (усреднение одного ряда соседних ячеек) и m = 2 (усреднение двух рядов). После трансформации, состоящей в усреднении ближайших узлов (левый график рис. 2.5.1), из трех оптимальных областей осталась только одна, расположенная в диапазоне от 28 до 34 дней по параметру «количество дней до экспирации» и 75–125 дней по параметру «период истории для расчета HV». Причина исчезновения двух других областей заключается в том, что их экстремумы оказались менее робастны, чем экстремум сохранившейся области. Трансформация, полученная путем усреднения большего количества узлов (правый график рис. 2.5.1), приводит к аналогичным результатам – исчезновению двух оптимальных областей и сохранению одной области оптимизационного пространства в качестве оптимальной. Таким образом, обе трансформации указывают на предпочтительность выбора одной и той же области. Данная область, помимо наибольшей робастности, имеет еще и наибольшую площадь. Это является дополнительным преимуществом для выбора оптимального решения в пределах именно этой области.

Хотя описанный в предыдущем разделе метод усреднения и учитывает при выборе оптимальной области ее высоту (значение целевой функции) и гладкость (робастность), но влияние первой величины перевешивает влияние второй. Предлагаемый в этом разделе метод придает робастности гораздо больший вес. В соответствии с данным методом значение целевой функции в каждом узле исходного оптимизационного пространства заменяется отношением среднего значения целевой функции группы узлов к стандартному отклонению, рассчитанному для этой же группы. Понятие «группы узлов» имеет тот же смысл, что и в процедуре усреднения. К группе относится сам узел и один, два, и т. д. рядов окружающих узлов. Такая трансформация поверхности учитывает как высотные отметки оптимальной области (числитель), так и гладкость ее рельефа (знаменатель).

На рис. 2.5.2 показаны две трансформации свертки, изображенной на рис. 2.4.1. Также как и в предыдущем разделе, трансформации строились с использованием одного и двух рядов соседних узлов ( m = 1 и m = 2 соответственно). При использовании одного ряда узлов (левый график рис. 2.5.2) возникает большое количество новых оптимальных областей (исходное оптимизационное пространство содержит всего три оптимальные области). Количество новых областей столь велико, что выбор одной из них практически невозможен. Эта проблема разрешается путем использования большей группы узлов (два ряда). В этом случае рельеф трансформированного оптимизационного пространства существенно упрощается (правый график рис. 2.5.2) и мы получаем всего три оптимальные области, из которых необходимо выбрать одну.

В отличие от трансформации методом усреднения (см. предыдущий раздел) ни одна из трех оптимальных областей не совпадает с оптимальными областями оригинального оптимизационного пространства. Это объясняется тем, что оптимальные области исходной свертки представляют собой узкие хребты и высокие пики. То есть эти области не достаточно робастны и обладают довольно ломанным рельефом. В противоположность этому три оптимальные области трансформированного пространства хоть и не расположены на самых высоких хребтах, зато находятся на достаточно гладких и широких плато средней высоты, что может быть предпочтительно с точки зрения их робастности. Поскольку эти три оптимальные области равноценны как по значению целевой функции, так и по робастности, выбрать из них одну можно по площади поверхности и по ее форме. При прочих равных условиях предпочтительно, чтобы оптимальная область имела большую площадь поверхности и более округлую форму (узкие области менее робастны по крайней мере по одному из параметров). Этим критериям соответствует область, расположенная в диапазоне 84–92 дней по параметру «количество дней до экспирации» и 155–175 дней по параметру «период истории для расчета HV».