Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

Рассмотрим устойчивость оптимизационного пространства базовой дельта-нейтральной стратегии по отношению к фиксированному параметру «порог критерия». На рис. 2.2.2 показана поверхность, полученная для целевой функции «прибыль» при условии, что порог критерия равен 1 %. Увеличим значение этого фиксированного параметра до 3 % и проверим, насколько такое изменение повлияет на форму оптимизационной поверхности.

Напомним, что до изменения фиксированного параметра глобальный максимум имел координаты 30 по параметру «число дней до экспирации» (горизонтальная ось графика) и 105 по параметру «период истории для расчета HV» (вертикальная ось). После увеличения значения фиксированного параметра глобальный максимум сместился и расположен в узле с координатами 16 и 120 соответственно. Учитывая общую площадь оптимизационного пространства, такое смещение глобального максимума нельзя назвать очень существенным (хотя оно безусловно не является пренебрежимо малым).

Исходное оптимизационное пространство имело единственную оптимальную область, протянувшуюся вдоль 30-й вертикали в диапазоне от 80 до 125 дней по параметру «период истории для расчета HV» (рис. 2.2.2). Левый график рис. 2.6.1 демонстрирует новое пространство, полученное в результате изменения фиксированного параметра. Прежняя оптимальная область сохранилась приблизительно на том же месте (незначительно сместившись вниз) и слегка увеличилась в размерах. Вместе с тем слева от оригинальной области появились четыре новые оптимальные области, две из которых очень маленькие, а две другие сопоставимы по размерам с прежней областью. Важно отметить, что, хотя количество оптимальных областей существенно выросло (пять вместо одной), все они располагаются приблизительно в левой нижней части оптимизационного пространства (12–36 дней по параметру «число дней до экспирации» и 40–180 по параметру «период истории для расчета HV»).

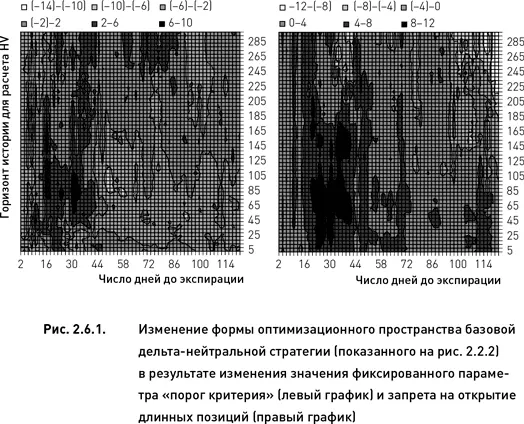
Из вышесказанного можно сделать вывод, что изменение фиксированного параметра не изменило принципиально форму оптимизационной поверхности. Это свидетельствует об относительной устойчивости оптимизационного пространства. Хотя произошедшие изменения могут показаться весьма существенными, необходимо принять во внимание, что изменение фиксированного параметра также было достаточно большим (с 1 % до 3 %). Мы специально использовали такое большое изменение, чтобы наглядно продемонстрировать видоизменение пространства. При тестировании устойчивости, производимой в ходе оптимизации автоматизированной стратегии, предназначенной для реальной торговли, можно ограничиться гораздо меньшими изменениями фиксированных параметров.

Понятие структурной устойчивости является очень широким. К структуре стратегии можно отнести практически все, начиная с базовой идеи и заканчивая относительно малозначительными техническими элементами. Изменение любого структурного элемента может коренным образом изменить форму оптимизационного пространства. Однако следует изначально ограничить область исследований структурной устойчивости. Интерес разработчика стратегии состоит в том, чтобы получаемое им оптимизационное пространство было устойчиво к небольшим изменениям структуры стратегии . Дело в том, что любое существенное изменение превращает оптимизируемую стратегию в совершенно другую стратегию, оптимизация которой, возможно, должна строиться совсем по-другому.

Примером небольших структурных изменений может быть метод распределения капитала или применение тех или иных инструментов управления рисками. Применительно к дельта-нейтральной стратегии, допустимое структурное изменение может заключаться, например, в изменении алгоритма расчета индексной дельты. С одной стороны, изменения этих и подобных им структурных элементов не меняет смысл стратегии. С другой стороны, желательно, чтобы оптимизационное пространство было устойчиво к изменениям такого рода. Например, если схема распределения капитала между элементами портфеля несколько изменяется и форма оптимизационного пространства не меняется коренным образом, то такая оптимизация является устойчивой и надежной. При этом следует помнить, что оптимизационное пространство может быть более устойчивым к одним структурным изменениям и менее устойчиво к другим.