Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

Для того чтобы результаты оптимизаций были сопоставимы (а также для того, чтобы было возможно построить свертку нескольких оптимизаций), необходимо чтобы значения целевой функции в каждом случае находились приблизительно в одном диапазоне. Это достигается с помощью трансформации, описанной в разделе, посвященном многокритериальному анализу (формула 2.4.1).

Сравнение 10 оптимизационных поверхностей (рис. 2.6.2, для простоты восприятия графиков показаны только оптимальные области) выявляет наличие двух устойчивых оптимальных областей, присутствующих почти на всех поверхностях. Одна из них расположена в районе 28–32 дней по параметру «количество дней до экспирации» и 85–140 дней по параметру «период истории для расчета HV» (будем условно называть эту область «левой»). Вторая оптимальная область имеет координаты 108–112 по первому параметру и 90–160 по второму (будем называть эту область «правой»).

Левая область присутствует на всех оптимизационных поверхностях, кроме двух– и трехлетней. Площадь ее поверхности достаточно стабильна (изменяясь весьма незначительно от случая к случаю). Исключение составляет только оптимизация, проведенная на однолетнем периоде. В этом случае левая область имеет большую площадь и, по сути, представляет собой три отдельные сгруппированные области.

Правая область также присутствует на всех оптимизационных поверхностях, за исключением единственного случая, когда оптимизация проводилась на десятилетнем периоде. Еще в двух случаях эта область оказалась несколько смещенной в область более высоких значений параметра «период истории для расчета HV». Площадь поверхности правой области более изменчива, чем площадь левой области. В оптимизациях, проведенных на 1-, 2-, 3-, 4– и 5-летнем периодах, правая область имеет довольно большие размеры. В противоположность этому на оптимизационных поверхностях, полученных на более продолжительных периодах, она имеет меньшую площадь поверхности. Кроме того, во всех случаях правая область не является единой, а раздроблена на большое количество субобластей.

Степень устойчивости оптимизационного пространства можно оценить разными методами. Самый простой из них – визуальный. Сравнение разных графиков рис. 2.6.2 в принципе указывает на то, что данная оптимизация достаточно устойчива. Это следует из описанного выше персистентного расположения оптимальных областей. Можно оценить степень устойчивости количественно, например, путем вычисления изменчивости координат узлов, составляющих оптимальные области.

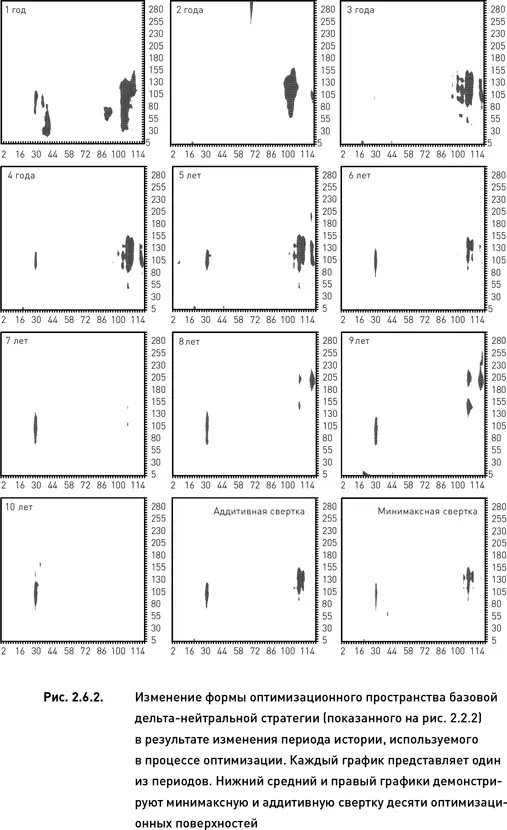
В том случае, когда устойчивость оценивается на основании сравнения большого количества оптимизационных поверхностей (как в нашем примере), можно использовать метод свертки. Идея заключается в том, что если поверхности очень отличаются друг от друга (то есть оптимизация является не устойчивой), то свертка таких поверхностей будет иметь большое количество беспорядочно разбросанных оптимальных областей. Если же оптимальные области располагаются на всех поверхностях приблизительно в одних и тех же местах (то есть если оптимизация устойчива), то свертка будет иметь одну или несколько четко обозначенных оптимальных областей. Нижний средний и правый графики рис. 2.6.2 демонстрируют аддитивную и минимаксную свертку десяти оптимизационных поверхностей (оба вида свертки оказались в данном случае почти идентичными). Левая и правая оптимальные области на этих свертках достаточно четко обозначены и локализованы, что еще раз подтверждает наш вывод об устойчивости оптимизации к изменению используемого периода истории.

До сих пор мы использовали самый информативный способ оптимизации – полный перебор всех возможных комбинаций параметров. Этот метод требует вычисления значений целевой функции во всех узлах оптимизационного пространства. Поскольку расчет целевой функции каждого узла требует сложных многоступенчатых вычислений, недостаток полного перебора состоит в большом количестве расчетов и времени требуемого для завершения полного оптимизационного цикла. С увеличением числа параметров количество расчетов и времени растет по степенному закону. Расширение области допустимых значений параметров и уменьшение шага оптимизации также увеличивают продолжительность времени, необходимого для полного перебора.