Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

Этот метод был разработан с целью уменьшить вероятность возникновения ситуаций, в которых метод покоординатного подъема останавливается преждевременно, не найдя удовлетворительного оптимального решения. Он включает в себя последовательное применение двух процедур – исследующего поиска и поиска по образцу, повторяемых до нахождения неулучшаемого оптимума. По сравнению с методом покоординатного подъема применение метода Хука−Дживса существенно сокращает вероятность остановки алгоритма, не достигнув экстремума. Алгоритм метода Хука−Дживса имеет следующий вид.

1. Выбирается стартовый узел. Начиная с этого узла, выполняется процедура исследующего поиска. Данная процедура заключается в исполнении нескольких циклов описанного выше метода покоординатного подъема. Один цикл исследующего поиска состоит из n циклов покоординатного поиска ( n – количество параметров). Для двумерного оптимизационного пространства требуется провести два цикла покоординатного подъема с тем, чтобы дополнительно к стартовому узлу найти два субоптимальных узла.

2. Выполняется процедура поиска по образцу. Для этого необходимо определить направление от стартового узла на найденный (в результате исполнения первого цикла исследующего поиска) узел. В этом направлении значение функции росло, и можно предположить, что, двигаясь далее в том же направлении, получим дальнейшее улучшение.

3. Выполняется процедура поиска в направлении, определенном на предыдущем этапе. В отличие от покоординатного подъема, данная оптимизация происходит при одновременном изменении всех параметров. Если в покоординатном подъеме движение возможно только по горизонтали или по вертикали (в двумерном случае), то поиск по образцу допускает движение вдоль любой прямой принадлежащей оптимизационной поверхности (или пространству в случае оптимизации более двух параметров).

4. Найдя наилучшую точку в этом направлении, повторяем цикл исследующего поиска, после чего вновь выполняем поиск по образцу, пока не достигнем точки, неулучшаемой ни на том, ни на другом этапе.

Рассмотрим применение метода Хука-Дживса на примере оптимизации базовой дельта-нейтральной стратегии по целевой функции «прибыль». По аналогии с предыдущим примером ограничим области допустимых значений параметров теми же диапазонами (2–80 для параметра «число дней до экспирации» и 100–300 для параметра «период истории для расчета HV»). Выполнение алгоритма происходит следующим образом:

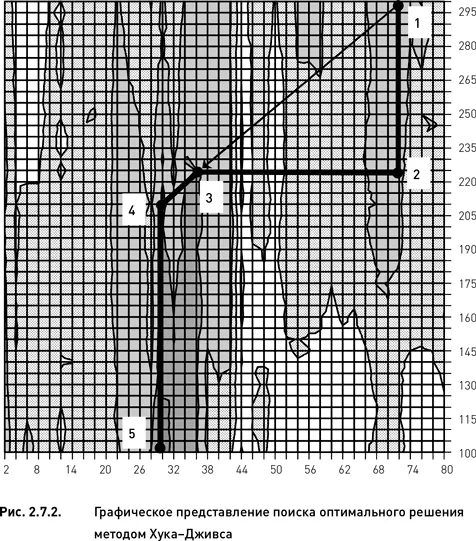
1. Случайным образом выбираем стартовую точку. Предположим, что был выбран узел с координатами 68 и 300. Данный узел отмечен номером 1 на рис. 2.7.2.

2. Начинаем процедуру исследующего поиска, заключающуюся в исполнении двух (по числу параметров) циклов покоординатного подъема. Зафиксировав параметр «число дней до экспирации» на значении 68, вычисляем целевую функцию для всех значений параметра «период истории для расчета HV». Определяем узел с максимальным значением целевой функции, каковым является узел с координатами 30 и 225 (точка номер 2 на рис. 2.7.2).

3. Фиксируем значение параметра «период истории для расчета HV» на значении 225 и вычисляем целевую функцию для всех значений параметра «число дней до экспирации». Максимальное значение функции приходится на узел с координатами 36 и 225 (третья точка).

4. Выполняем процедуру поиска по образцу. Определяем направление от стартового узла (номер 1) на узел 3 (стрелка на рис. 2.7.2) и выполняем одномерную оптимизацию в найденном направлении. Вычисляем значение целевой функции во всех узлах, пересекаемых диагональю в заданном направлении.

5. Выбираем узел с максимальным значением целевой функции (четвертая точка с координатами 30 и 210). Начиная с этого узла, повторяем цикл исследующего поиска.

6. Фиксируем значение параметра «число дней до экспирации» на значении 30 и вычисляем целевую функцию для всех значений параметра «период истории для расчета HV». Максимальное значение функции оказывается в узле с координатами 30 и 105 (пятая точка).

7. Фиксируем период истории на значении 105 и вычисляем целевую функцию для всех дней до экспирации. Выясняем, что дальнейшего улучшения не происходит и, следовательно, алгоритм останавливается. Оптимальным решением является узел номер 5.