Вадим Цудикман - Опционы - Разработка, оптимизация и тестирование торговых стратегий

Примером полимодального оптимизационного пространства может служить линия, полученная в том случае, когда параметр «число дней до экспирации» был зафиксирован на значении «108 дней». Глобальный максимум этой оптимизации приходится на значение «145 дней» параметра «период истории для расчета HV». В отличие от предыдущего примера целевая функция этого оптимизационного пространства имеет явно выраженный локальный максимум, приходящийся на «205 дней» параметра «период истории для расчета HV».

И, наконец, третья линия на рис. 2.2.1 является примером безмодального оптимизационного пространства. В том случае, когда сигналы на открытие торговых позиций генерировались только для краткосрочных опционов (параметр «число дней до экспирации» зафиксирован на значении «четыре дня»), целевая функция оказалась приблизительно нулевой почти для всего диапазона параметра «горизонт истории».

Поскольку в примерах, приведенных на рис. 2.2.1, целевая функция была исследована на всем диапазоне допустимых значений параметра (так называемый метод полного перебора), то выбор оптимального решения на первый взгляд кажется очевидным. Для унимодальной функции – это 120 дней, для полимодальной – 145 дней. Однако оптимальное решение не обязательно должно совпадать с глобальным или локальным экстремумом. Существует дополнительный, не менее важный критерий выбора оптимального решения – его робастность. Принимая во внимание понятие робастности, выбор 120 дней в качестве оптимального решения может оказаться не самым лучшим. Увеличение параметра (до 125, 130 и т. д.) ведет к достаточно резкому падению целевой функции. В то же время если в качестве оптимального решения выбрать 195 дней, то все соседние значения параметра (как в сторону увеличения, так и в сторону уменьшения) имеют достаточно высокие значения целевой функции. В данном примере глобальный максимум унимодальной функции полезности является более робастным оптимальным решением (он находится на более широком возвышении), чем глобальный максимум полимодальной функции (который расположен на достаточно узком пике).

В дальнейшем мы будем рассматривать примеры, относящиеся к двумерной оптимизации. Будем использовать те же два параметра, что и в предыдущем примере: период истории для расчета HV (параметр, который оптимизировали в предыдущем примере) и количество дней до экспирации опционов (значения этого параметра были зафиксированы). Для первого параметра область допустимых значений находится в диапазоне от пяти до 300 дней, шаг оптимизации – пять дней. Для количества дней до экспирации диапазон значений составляет от двух до 120 дней, шаг оптимизации – два дня. Таким образом, полное оптимизационное пространство состоит из 3600 узлов (60 × 60).

На рис. 2.2.2 показано двумерное оптимизационное пространство целевой функции «средняя прибыль». Одномерные пространства, обсуждавшиеся ранее, представляют собой три частных случая этого двумерного пространства. Поскольку рис. 2.2.2 представляет собой топографическую карту, то вертикальные разрезы, проведенные по значениям 4, 32 и 108 параметра «число дней до экспирации», совпадают с профилями одномерных пространств, показанных на рис. 2.2.1. Несомненно, двумерное оптимизационное пространство позволяет получить лучшее представление о целевой функции и обо всей торговой стратегии в целом.

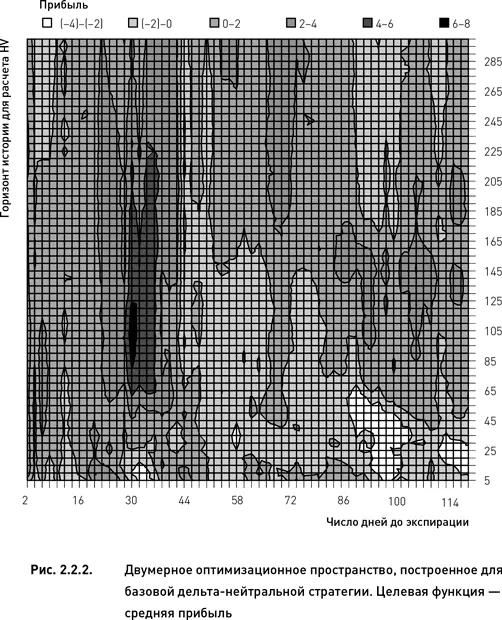
Глобальный максимум оптимизационного пространства, представленного на рис. 2.2.2, имеет координаты 30 по горизонтальной оси и 105 по вертикальной. Это означает, что средняя прибыль (то есть целевая функция) достигает своего максимума в том случае, когда позиции открываются, используя опционы, до истечения которых остается 30 дней, а историческая волатильность, используемая для расчета критерия, оценивается на историческом периоде длиной 105 дней. Данный глобальный максимум расположен на вершине небольшого «хребта», протянувшегося вдоль 30-й вертикали (параметр «число дней до экспирации») в диапазоне от 80 до 125 (параметр «горизонт истории для расчета IV»).

Данный хребет можно рассматривать, как оптимальную область, поскольку все узлы, расположенные в пределах этой зоны, имеют высокое значение целевой функции (> 6 %). Сама оптимальная область также окружена достаточно широкой областью, состоящей из узлов с относительно высокими значениями целевой функции. Поэтому найденное оптимальное решение можно в принципе считать робастным. Однако следует оговориться, что робастность оптимального решения неодинакова по двум параметрам. Изменения значений параметра «период истории для расчета HV» в пределах оптимальной зоны и вокруг нее приводят к меньшим изменениям целевой функции, чем изменения параметра «число дней до экспирации» (при отступлении от оптимального значения этого параметра [30 дней] в большую или меньшую сторону происходит резкое снижение целевой функции). Следовательно, робастность первому параметру выше робастности по второму.