John Long - Darwin’s Devices

We think these simplifications were justified, but we must always be on guard against simplifications that are not. If we ever cannot justify them to other people, then we have failed in our primary goal: to test an evolutionary hypothesis of animals using robots as model simulations.

Last comes the justification. Barbara Webb delineates seven dimensions that can be used to help describe and characterize biorobotic models: (1) biological relevance , (2) match between the behavior of the biological target and the robot model, (3) accuracy of the model in using the same functional mechanisms as the target, (4) how concrete the model is in terms of mimicking features of the target, (5) the level in the target’s structural hierarchy at which the model focuses, (6) the specificity of the model in terms of the number of elements targeted, and (7) the substrate from which the model is built, either digital or physical. [30] Barbara Webb, “Can Robots Make Good Models of Biological Behaviour?” Behavioural and Brain Sciences 24, no. 6 (2001): 1033–1050. Also see Webb, “Validating Biorobotic Models,” Journal of Neural Engineering 3, no. 3 (September 2006): R25–R35. I use my rephrased terms of Webb’s dimensions in my paper “Biomimetic Robotics: Self-Propelled Physical Models Test Hypotheses about the Mechanics and Evolution of Swimming Vertebrates,” Proceedings of the Institution of Mechanical Engineers, Part C, Journal of Mechanical Engineering Science 221, no. 10 (2007): 1193–1200.

For Webb, the key dimensions for biorobotic models are biological relevance and substrate. You’ve got to have a robotic system that allows you to test a hypothesis about your target or it isn’t relevant; the test of the hypothesis can be if the robotic system works as expected or, in the case of Evolutionary Biorobotics, if the evolutionary trajectory of the system is as expected. Moreover, she argues that the substrate ought to be physical rather than digital, for all the reasons outlined in Chapter 1.

For Evolutionary Biorobotics models, we include behavioral match and functional accuracy. For example, we want an individual Tadro3 to behave like a tunicate tadpole in terms of (1) using a tail that generates thrust by undulating, (2) navigating up a light gradient, and (3) being part of an interacting and evolving population. That’s the behavioral match, with a three-layer nested hierarchy of the behavior of the organ, the individual, and the population.

We also want Tadro3 to use the same functional mechanisms that tunicate tadpoles do, such as the same kind of undulatory wiggle of the tail and the same neural wiring and sensorimotor loops that we’ve understood and engineered above. We also want the evolutionary mechanisms that we talked about in Chapter 2—selection, mutation, random mating, and genetic drift—to be what drives the evolution of the population of Tadro3s. That’s the accuracy of the functional mechanisms, with a three-layer hierarchy of propulsive mechanism, sensory-neural-motor mechanism, and evolutionary mechanisms.

In sum, relevance, substrate, match, and accuracy are our primary goals for designing, engineering, and running Tadro3s as a model simulation of the earliest fish-like vertebrates. We’ll judge how close we come to meeting those goals when we look at the Tadro3s playing the game of life in their water world in Chapter 4.

Throughout this design process we’ve employed the KISS principle and simplified our Evolvabot and its world whenever we could. We’ve even argued in the scientific literature that the original Tadro1, which was built to swim and behave like a tunicate tadpole, is the simplest possible autonomous navigator because it possesses a single sensor and a single motor control output (tail offset to turn). Tadro3 has that same basic hardware and neural architecture but has the biomimetic tail coded to evolve. Simple, simple.

But as we’ve seen, even with a simple robot like Tadro3, you need to understand a ton of stuff about the animal target. Think: the engineers’ code. Think: specifications. We had to figure out how evolution works (Chapter 2), make an educated guess about the hypothetical chordate ancestor of vertebrates, find a reasonable living proxy for that ancestor (tunicate tadpole larva), understand the swimming behavior of the tadpole, infer the neural control system of the tadpole, measure the mechanical function of a tail with a notochord, and divine a likely selection pressure on early vertebrates. Phew (pant, pant, out of breath …)! This is the kind of understanding that allows us to follow the secret engineers’ code and build a population of evolving robots.

But were we successful?

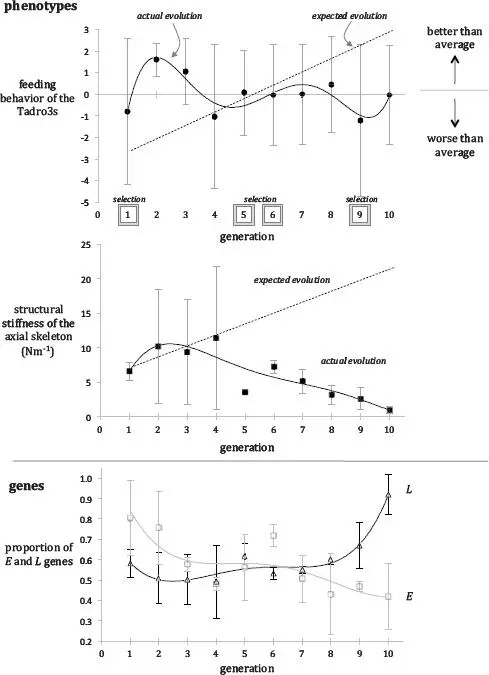
TADROS EVOLVE! BY ANY MEASURE, OUR POPULATION of autonomous, aquatic Evolvabots successfully played the game of life (Figure 4.1). No surprise, I hope—indeed, the surprise would have been if they didn’t evolve, as that was what we designed them to do.

If you begin at the beginning and then go on until you get to the end, [31] Plagiarism detector alert: a thank you to Lewis Carroll. you would see that from the design of Tadro1 in 2003 to the publication of our Tadro3 paper in 2006, our Tadro team had more than twenty-three members. Okay, so that’s not a small-to mediumsized village. But it’s still some measure of how hard this work is.

Kira Irving, Keon Combie, Virginia Engel, and Joe Schumacher led a group of Tadro3 operators and biomimetic tail benders that included Nicole Doorly, Yusuke Kumai, Gianna McArthur, and Kurt Bantilan. They performed 120 trials over ten generations, building 360 tails with biomimetic backbones along the way. Each trial also had three minutes of videotape to analyze in one-second increments; in each frame, we had to mark (and then double-check) the position of the light and the bow and the stern of each Tadro3. We used these points to compute average speed, average wobble, time to the food, and average distance to the light source. Twelve of these numbers for each individual tail phenotype (each phenotype was described by two traits: length of tail, L , and the biomimetic notochord’s material stiffness, E —more on these later) were then used to calculate the three individual fitnesses corresponding to each phenotype—fitnesses that we needed to run the genetic algorithm that spat out the next generation’s phenotypes. When we were really cranking full time in the summer—including evenings—a group of four or five of us could get a generation done in about four days. But if anything went wrong, like when we dropped a Tadro upside-down in the water, then we’d have to stop and rebuild before we could get back to the evolutionary trials. All told, the trials took ten weeks.

As we let our population of Tadro3s play its game of life, we found that the feeding behavior, tail stiffness, and genetic composition of the population all changed over generational time (Figure 4.1). Although the fact that the population evolved wasn’t a surprise, we were surprised about the direction evolution took. I should say directions, plural. Under a steady selection pressure that rewarded enhanced feeding behavior, we expected steady, directional change. Instead, what we see, even in this simplified Tadro3 world, is that evolutionary change oscillates, moving in different directions at different times.